
科目: 来源: 题型:解答题
一个均匀的正方体玩具,各个面上分别写有1,2,3,4,5,6,将这个玩具先后抛掷2次,求:
(1)朝上的一面数相等的概率;(2)朝上的一面数之和小于5的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
中国2010年上海世博会已于2010年5月1日在上海隆重开馆.小王某天乘火车从重庆到上海去参观世博会,若当天从重庆到上海的三列火车正点到达的概率分别为0.8、0.7、0.9,假设这三列火车之间是否正点到达互不影响.求:
(1)这三列火车恰好有两列正点到达的概率;
(2)这三列火车至少有一列正点到达的概率
查看答案和解析>>
科目: 来源: 题型:解答题
某同学在生物研究性学习中想对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
| 日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差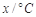 | 10 | 11 | 13 | 12 | 8 |
发芽数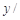 颗 颗 | 23 | 25 | 30 | 26 | 16 |
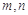 ,求事件“
,求事件“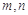 均不小于25的概率。
均不小于25的概率。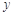 关于
关于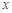 的线性回归方程
的线性回归方程 ;
;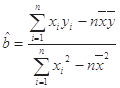 ,
,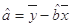 )
)查看答案和解析>>
科目: 来源: 题型:解答题
某县为增强市民的环境保护意识,面向全县征召义务宣传志愿者,先从符合条件的志愿者中随机抽取100名按年龄分组:第1组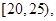 第2组
第2组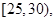 第3组
第3组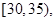 第4组
第4组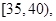 第5组
第5组 得到的频率分布直方图如图所示,
得到的频率分布直方图如图所示,
(1)分别求第3,4,5组的频率。
(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参与广场的宣传活动,应从第3,4,5组各抽取多少名志愿者.
(3)在(2)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.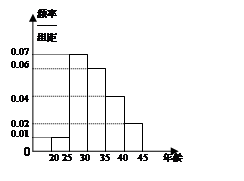
查看答案和解析>>
科目: 来源: 题型:解答题
下图是淮北市6月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择6月1日至6月15日中的某一天到达该市,并停留2天.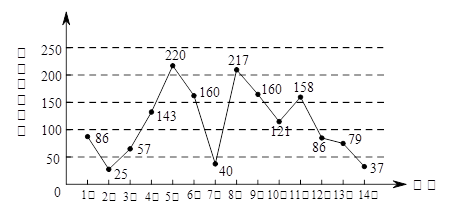
(1)求此人到达当日空气重度污染的概率;
(2)若设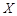 是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
(3)由图判断从哪天开始淮北市连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次任意抽取3道题,独立作答,然后由乙回答剩余3题,每人答对其中的2题就停止答题,即闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是 .
.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某校举行综合知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有6次答题的机会,选手累计答对4题或答错3题即终止其初赛的比赛,答对4题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题连续两次答错的概率为 (已知甲回答每道题的正确率相同,并且相互之间没有影响).
(已知甲回答每道题的正确率相同,并且相互之间没有影响).
(Ⅰ)求选手甲回答一个问题的正确率;
(Ⅱ)求选手甲可以进入决赛的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
两人约定在20:00到21:00之间相见,并且先到者必须等迟到者40分钟方可离去,如果两人出发是各自独立的,在20:00到21:00各时刻相见的可能性是相等的,求两人在约定时间内相见的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取一个,求:(Ⅰ)连续取两次都是白球的概率;(Ⅱ)若取一个红球记2分,取一个白球记1分,取一个黑球记0 分,连续取三次分数之和为4分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com