
科目: 来源: 题型:解答题
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数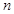 及天数如下表:
及天数如下表:
售出个数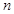 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
查看答案和解析>>
科目: 来源: 题型:解答题
一个口袋中装有大小形状完全相同的红色球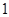 个、黄色球
个、黄色球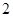 个、蓝色球
个、蓝色球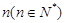 个.现进行从口袋中摸球的游戏:摸到红球得
个.现进行从口袋中摸球的游戏:摸到红球得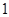 分、摸到黄球得
分、摸到黄球得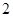 分、摸到蓝球得
分、摸到蓝球得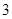 分.若从这个口袋中随机地摸出
分.若从这个口袋中随机地摸出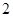 个球,恰有一个是黄色球的概率是
个球,恰有一个是黄色球的概率是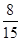 .
.
⑴求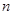 的值;⑵从口袋中随机摸出
的值;⑵从口袋中随机摸出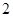 个球,设
个球,设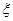 表示所摸
表示所摸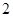 球的得分之和,求
球的得分之和,求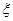 的分布列和数学期望
的分布列和数学期望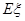 .
.
查看答案和解析>>
科目: 来源: 题型:解答题
某工厂在试验阶段大量生产一种零件,这种零件有 、
、 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为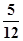 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为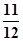 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(1)求一个零件经过检测为合格品的概率是多少?
(2)任意依次抽取该种零件 个,设
个,设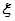 表示其中合格品的个数,求
表示其中合格品的个数,求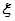 的分布列及数学期望
的分布列及数学期望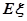 .
.
查看答案和解析>>
科目: 来源: 题型:解答题
有甲、乙两个班进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表:
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 总计 | | | 210 |
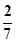 .
. ,其中
,其中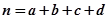 .
.| 参考数据 | 当 ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
当 >2.706时,有90%的把握判定变量A,B有关联; >2.706时,有90%的把握判定变量A,B有关联; | |
当 >3.841时,有95%的把握判定变量A,B有关联; >3.841时,有95%的把握判定变量A,B有关联; | |
当 >6.635时,有99%的把握判定变量A,B有关联. >6.635时,有99%的把握判定变量A,B有关联. |
查看答案和解析>>
科目: 来源: 题型:解答题
一个袋中装有8个大小质地相同的球,其中4个红球、4个白球,现从中任意取出四个球,设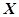 为取得红球的个数.
为取得红球的个数.
(1)求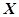 的分布列;
的分布列;
(2)若摸出4个都是红球记5分,摸出3个红球记4分,否则记2分.求得分的期望.
查看答案和解析>>
科目: 来源: 题型:解答题
如图,某中学甲、乙两班共有25名学生报名参加了一项 测试.这25位学生的考分编成的茎叶图,其中有一个数据因电脑操作员不小心删掉了(这里暂用x来表示),但他清楚地记得两班学生成绩的中位数相同.
(1)求这两个班学生成绩的中位数及x的值;
(2)如果将这些成绩分为“优秀”(得分在175分以上,包括175分)和“过关”,若学校再从这两个班获得“优秀”成绩的考生中选出3名代表学校参加比赛,求这3人中甲班至多有一人入选的概率.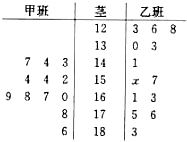
查看答案和解析>>
科目: 来源: 题型:解答题
某家电专卖店在五一期间设计一项有奖促销活动,每购买一台电视,即可通过电脑产生一组3个数的随机数组,根据下表兑奖:
| 奖次 | 一等奖 | 二等奖 | 三等奖 |
| 随机数组的特征 | 3个1或3个0 | 只有2个1或2个0 | 只有1个1或1个0 |
| 资金(单位:元) | 5m | 2m | m |
查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙两人玩一种游戏;在装有质地、大小完全相同,编号分别为1,2,3,4,5,6六个球的口袋中,甲先模出一个球,记下编号,放回后乙再模一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(1)求甲赢且编号和为8的事件发生的概率;
(2)这种游戏规则公平吗?试说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
2008年5月12日,四川汶川发生8.0级特大地震,通往灾区的道路全部中断. 5月12日晚,抗震救灾指挥部决定从水路(一支队伍)、陆路(东南和西北两个方向各一支队伍)和空中(一支队伍)同时向灾区挺进.在5月13日,仍时有较强余震发生,天气状况也不利于空中航行. 已知当天从水路抵达灾区的概率是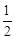 ,从陆路每个方向抵达灾区的概率都是
,从陆路每个方向抵达灾区的概率都是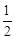 ,从空中抵达灾区的概率是
,从空中抵达灾区的概率是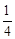 .
.
(1)求在5月13日恰有1支队伍抵达灾区的概率;
(2)求在5月13日抵达灾区的队伍数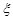 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com