
科目: 来源: 题型:解答题
某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
| 运行次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2 100 | 1 027 | 376 | 697 |
| 运行次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2 100 | 1 051 | 696 | 353 |
查看答案和解析>>
科目: 来源: 题型:解答题
受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
| 品牌 | 甲 | | | 乙 | |
| 首次出现故障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
| 轿车数量(辆) | 2 | 3 | 45 | 5 | 45 |
| 每辆利润(万元) | 1 | 2 | 3 | 1.8 | 2.9 |
查看答案和解析>>
科目: 来源: 题型:解答题
如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
(1)求此人到达当日空气质量优良的概率;
(2)求此人在该市停留期间只有1天空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目: 来源: 题型:解答题
为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:解答题
现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(1)求这4个人中恰有2人去参加甲游戏的概率;
(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(3)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X Y|,求随机变量ξ的分布列与数学期望Eξ.
查看答案和解析>>
科目: 来源: 题型:解答题
在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,设O为坐标原点,点P的坐标为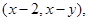 记
记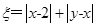 .
.
(1)求随机变量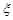 的最大值,并求事件“
的最大值,并求事件“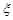 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量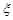 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙二人参加知识竞答,共有10个不同的题目,其中选择题6个,判断题4个,甲、乙二人依次各抽一题,那么
(1)甲抽到选择题,乙抽到判断题的概率是多少?
(2)甲、乙二人中至少有一个抽到选择题的概率是多少?
查看答案和解析>>
科目: 来源: 题型:解答题
“光盘行动”倡导厉行节约,反对铺张浪费,带动大家珍惜粮食,吃光盘子中的食物,得到从中央到民众的支持,为了解某地响应“光盘行动”的实际情况,某校几位同学组成研究性学习小组,从某社区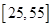 岁的人群中随机抽取n人进行了一次调查,得到如下统计表:
岁的人群中随机抽取n人进行了一次调查,得到如下统计表: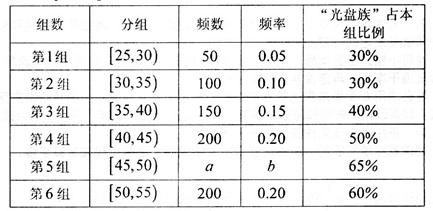
(1)求a,b的值,并估计本社区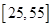 岁的人群中“光盘族”所占比例;
岁的人群中“光盘族”所占比例;
(2)从年龄段在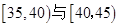 的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.
的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.
(1)已知选取2人中1人来自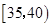 中的前提下,求另一人来自年龄段
中的前提下,求另一人来自年龄段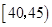 中的概率;
中的概率;
(2)求2名领队的年龄之和的期望值(每个年龄段以中间值计算).
查看答案和解析>>
科目: 来源: 题型:解答题
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
| 甲 | | 乙 |
| 6 | 9 | 3 6 7 9 9 |
| 9 5 1 0 | 8 | 0 1 5 6 |
| 9 9 4 4 2 | 7 | 3 4 5 8 8 8 |
| 8 8 5 1 1 0 | 6 | 0 7 7 |
| 4 3 3 2 | 5 | 2 5 |
| | 甲班(A方式) | 乙班(B方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |
 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:解答题
一种电脑屏幕保护画面,只有符号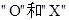 随机地反复出现,每秒钟变化一次,每次变化只出现
随机地反复出现,每秒钟变化一次,每次变化只出现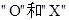 之一,其中出现
之一,其中出现 的概率为p,出现
的概率为p,出现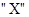 的概率为q,若第k次出现
的概率为q,若第k次出现 ,则记
,则记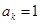 ;出现
;出现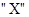 ,则记
,则记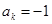 ,令
,令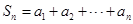 .
.
(1)当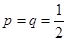 时,求
时,求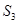 的分布列及数学期望.
的分布列及数学期望.
(2)当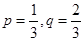 时,求
时,求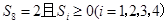 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com