
科目: 来源: 题型:解答题
电视台综艺频道组织的闯关游戏,游戏规定前两关至少过一关才有资格闯第三关,闯关者闯第一关成功得3分,闯第二关成功得3分,闯第三关成功得4分.现有一位参加游戏者单独闯第一关、第二关、第三关成功的概率分别为 、
、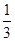 、
、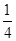 ,记该参加者闯三关所得总分为ξ.
,记该参加者闯三关所得总分为ξ.
(1)求该参加者有资格闯第三关的概率;
(2)求ξ的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为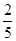 ,中奖可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率.
,中奖可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门.该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同.
(1)求3个学生选择了3门不同的选修课的概率;
(2)求恰有2门选修课这3个学生都没有选择的概率;
(3)设随机变量X为甲、乙、丙这三个学生选修数学史这门课的人数,求X的分布列.
查看答案和解析>>
科目: 来源: 题型:解答题
设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列.
查看答案和解析>>
科目: 来源: 题型:解答题
有一种闯三关游戏规则规定如下:用抛掷正四面体型骰子(各面上分别有1,2,3,4点数的质地均匀的正四面体)决定是否过关,在闯第n(n=1,2,3)关时,需要抛掷n次骰子,当n次骰子面朝下的点数之和大于n2时,则算闯此关成功,并且继续闯关,否则停止闯关.每次抛掷骰子相互独立.
(1)求仅闯过第一关的概率;
(2)记成功闯过的关数为ξ,求ξ的分布列.
查看答案和解析>>
科目: 来源: 题型:解答题
A高校自主招生设置了先后三道程序:部分高校联合考试、本校专业考试、本校面试.在每道程序中,设置三个成绩等级:优、良、中.若考生在某道程序中获得“中”,则该考生在本道程序中不通过,且不能进入下面的程序.考生只有全部通过三道程序,自主招生考试才算通过.某中学学生甲参加A高校自主招生考试,已知该生在每道程序中通过的概率均为 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2.
(1)求学生甲不能通过A高校自主招生考试的概率;
(2)设ξ为学生甲在三道程序中获优的次数,求ξ的分布列.
查看答案和解析>>
科目: 来源: 题型:解答题
袋中装有若干个质地均匀大小一致的红球和白球,白球数量是红球数量的两倍.每次从袋中摸出一个球然后放回,若累计3次摸到红球则停止摸球,否则继续摸球直至第5次摸球后结束.
(1)求摸球3次就停止的事件发生的概率;
(2)记摸到红球的次数为 ,求随机变量
,求随机变量 的分布列及其期望.
的分布列及其期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有 两条巷道通往作业区(如下图),
两条巷道通往作业区(如下图), 巷道有
巷道有 三个易堵塞点,各点被堵塞的概率都是
三个易堵塞点,各点被堵塞的概率都是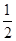 ;
; 巷道有
巷道有 两个易堵塞点,被堵塞的概率分别为
两个易堵塞点,被堵塞的概率分别为 .
.
(1)求 巷道中,三个易堵塞点最多有一个被堵塞的概率;
巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若 巷道中堵塞点个数为
巷道中堵塞点个数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 ,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
低碳生活,从“衣食住行”开始.在国内一些网站中出现了“碳足迹”的应用,人们可以由此计算出自己每天的碳排放量,如家居用电的二氧化碳排放量(千克)=耗电度数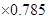 ,家用天然气的二氧化碳排放量(千克)=天然气使用立方数
,家用天然气的二氧化碳排放量(千克)=天然气使用立方数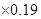 等.某校开展“节能减排,保护环境,从我做起!”的活动,该校高一、六班同学利用假期在东城、西城两个小区进行了逐户的关于“生活习惯是否符合低碳排放标准”的调查.生活习惯符合低碳观念的称为“低碳家庭”,否则称为“非低碳家庭”.经统计,这两类家庭占各自小区总户数的比例
等.某校开展“节能减排,保护环境,从我做起!”的活动,该校高一、六班同学利用假期在东城、西城两个小区进行了逐户的关于“生活习惯是否符合低碳排放标准”的调查.生活习惯符合低碳观念的称为“低碳家庭”,否则称为“非低碳家庭”.经统计,这两类家庭占各自小区总户数的比例 数据如下:
数据如下:
(1)如果在东城、西城两个小区内各随机选择2个家庭,求这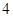 个家庭中恰好有两个家庭是“低碳家庭”的概率;
个家庭中恰好有两个家庭是“低碳家庭”的概率;
(2)该班同学在东城小区经过大力宣传节能减排的重要意义,每周“非低碳家庭”中有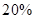 的家庭能加入到“低碳家庭”的行列中.宣传两周后随机地从东城小区中任选
的家庭能加入到“低碳家庭”的行列中.宣传两周后随机地从东城小区中任选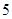 个家庭,记
个家庭,记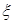 表示
表示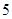 个家庭中“低碳家庭”的个数,求
个家庭中“低碳家庭”的个数,求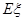 和
和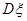 .
.
查看答案和解析>>
科目: 来源: 题型:解答题
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.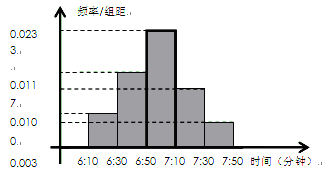
(1)根据图中的数据信息,求出众数 和中位数
和中位数 (精确到整数分钟);
(精确到整数分钟);
(2)小明的父亲上班离家的时间 在上午
在上午 之间,而送报人每天在
之间,而送报人每天在 时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件
时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件 )的概率.
)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com