
科目: 来源: 题型:解答题
为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表:
| 评估的平均得分 | 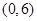 | 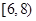 | 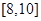 |
| 全市的总体交通状况等级 | 不合格 | 合格 | 优秀 |
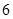 条道路中抽取
条道路中抽取 条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过
条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过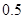 的概率.
的概率.查看答案和解析>>
科目: 来源: 题型:解答题
一个口袋中有 个白球和
个白球和 个红球(
个红球( ,且
,且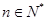 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率 ;
;
(2)若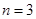 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为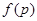 ,当
,当 为何值时,
为何值时,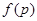 取最大值.
取最大值.
查看答案和解析>>
科目: 来源: 题型:解答题
某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查.调查问卷共10道题,答题情况如下表:
| 答对题目数 |  | 8 | 9 |  |
| 女 | 2 | 13 | 12 | 8 |
| 男 | 3 | 37 | 16 | 9 |
查看答案和解析>>
科目: 来源: 题型:解答题
为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:
| 甲公司某员工A | | 乙公司某员工B | ||||||||||||
| 3 | 9 | 6 | 5 | 8 | 3 | 3 | 2 | 3 | 4 | 6 | 6 | 6 | 7 | 7 |
| | | | | | | 0 | 1 | 4 | 4 | 2 | 2 | 2 | | |
 (单位:元),求
(单位:元),求 的分布列和数学期望;
的分布列和数学期望;查看答案和解析>>
科目: 来源: 题型:解答题
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为 .
.
(1)求直线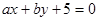 与圆
与圆 相切的概率;
相切的概率;
(2)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求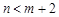 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙、丙、丁4名同学被随机地分到 三个社区参加社会实践,要求每个社区至少有一名同学.
三个社区参加社会实践,要求每个社区至少有一名同学.
(1)求甲、乙两人都被分到 社区的概率;
社区的概率;
(2)求甲、乙两人不在同一个社区的概率;
(3)设随机变量 为四名同学中到
为四名同学中到 社区的人数,求
社区的人数,求 的分布列和
的分布列和 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:解答题
某校举行中学生“日常生活小常识”知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有5次答题机会,选手累计答对3题或答错3题即终止比赛,答对3题者直接进入复赛,答错3题者则被淘汰.已知选手甲答对每个题的概率均为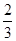 ,且相互间没有影响.
,且相互间没有影响.
(1)求选手甲进入复赛的概率;
(2)设选手甲在初赛中答题的个数为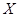 ,试求
,试求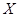 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com