
科目: 来源: 题型:解答题
1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,问从2号箱取出红球的概率是多少?
查看答案和解析>>
科目: 来源: 题型:解答题
抛掷红、蓝两颗骰子,设事件A为“蓝色骰子的点数为3或6”,事件B为“两颗骰子的点数之和大于8”.
(1)求P(A),P(B),P(AB);
(2)当已知蓝色骰子的点数为3或6时,求两颗骰子的点数之和大于8的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
某超市在节日期间进行有奖促销,凡在该超市购物满400元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球.顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就继续摸球.规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次停止摸奖的概率;
(2)记 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 的分布律和数学期望.
的分布律和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
对一批共50件的某电器进行分类检测,其重量(克)统计如下:
| 重量段 | [80,85) | [85,90) | [90,95) | [95,100] |
| 件数 | 5 | a | 15 | b |
查看答案和解析>>
科目: 来源: 题型:解答题
为了倡导健康、低碳、绿色的生活理念,某市建立了公共自行车服务系统鼓励市民租用公共自行车出行公共自行车按每车每次的租用时间进行收费,具体收费标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,收费1元;
③租用时间为2小时以上且不超过3小时,收费2元;
④租用时间超过3小时的时段,按每小时2元收费(不足1小时的部分按1小时计算)已知甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5 ,租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
(1)求甲、乙两人所付租车费相同的概率;
(2)设甲、乙两人所付租车费之和为随机变量 ,求
,求 的分布列和数学期望E
的分布列和数学期望E
查看答案和解析>>
科目: 来源: 题型:解答题
A、B两个投资项目的利润率分别为随机变量X1和X2,根据市场分析,X1和X2的分布列分别为
| X1 | 5% | 10% |
| P | 0.8 | 0.2 |
| X2 | 2% | 8% | 12% |
| P | 0.2 | 0.5 | 0.3 |
查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙两名射手各打了10发子弹,其中甲击中环数与次数如下表
| 环数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 次数 | 1 | 1 | 1 | 1 | 2 | 4 |
| 环数 | 7 | 8 | 9 | 10 |
| 概率 | 0.2 | 0.3 | p | 0.1 |
查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率为
,乙每次击中目标的概率为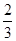 .
.
(1)求乙至多击中目标2次的概率;
(2)记甲击中目标的次数为Z,求Z的分布列、数学期望和标准差.
查看答案和解析>>
科目: 来源: 题型:解答题
某地位于甲、乙两条河流的交汇处,根据统计资料预测,今年汛期甲河流发生洪水的概率为0.25,乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响).现有一台大型设备正在该地工作,为了保护设备,施工部门提出以下三种方案:
方案1:运走设备,此时需花费4000元;
方案2:建一保护围墙,需花费1000元,但围墙只能抵御一个河流发生的洪水,当两河流同时发生洪水时,设备仍将受损,损失约56000元;
方案3:不采取措施,此时,当两河流都发生洪水时损失达60000元,只有一条河流发生洪水时,损失为10000元.
(1)试求方案3中损失费X(随机变量)的分布列;
(2)试比较哪一种方案好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com