
科目: 来源: 题型:解答题
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
| 指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
| 频数 | 8 | 20 | 42 | 22 | 8 |
| 指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
| 频数 | 4 | 12 | 42 | 32 | 10 |
 从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)查看答案和解析>>
科目: 来源: 题型:解答题
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值;
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
在打靶训练中,某战士射击一次的成绩在9环(包括9环)以上的概率是0.18,在8~9环(包括8环)的概率是0.51,在7~8环(包括7环)的概率是0.15,在6~7环(包括6环)的概率是0.09.计算该战士在打靶训练中射击一次取得8环(包括8环)以上成绩的概率和该战士打靶及格(及格指6环以上包括6环)的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
在打靶训练中,某战士射击一次的成绩在9环(包括9环)以上的概率是0.18,在8~9环(包括8环)的概率是0.51,在7~8环(包括7环)的概率是0.15,在6~7环(包括6环)的概率是0.09.计算该战士在打靶训练中射击一次取得8环(包括8环)以上成绩的概率和该战士打靶及格(及格指6环以上包括6环)的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
甲乙二人用4张扑克牌(分别是红桃2,红桃3,红桃4,方片4)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(1)设 ,
,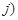 表示甲乙抽到的牌的数字,
表示甲乙抽到的牌的数字, 如甲抽到红桃2,乙抽到红桃3,记为
如甲抽到红桃2,乙抽到红桃3,记为 ,
,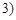 ,写出甲乙二人抽到的牌的所有情况;
,写出甲乙二人抽到的牌的所有情况;
(2)若甲抽到红桃3,则乙抽出的牌面数字比3大的概率是多少?
(3)甲乙约定,若甲抽到的牌的牌面数字比乙大,则甲胜;否则,乙胜,你认为此游戏是否公平?请说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
某中学从高中三个年级选派4名教师和20名学生去当文明交通宣传志愿者,20名学生的名额分配为高一12人,高二6人,高三2人.
(1)若从20名学生中选出3人做为组长,求他们中恰好有1人是高一年级学生的概率;
(2)若将4名教师随机安排到三个年级(假设每名教师加入各年级是等可能的,且各位教师的选择是相互独立的),记安排到高一年级的教师人数为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、 人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
(1)求 的值;
的值;
(2)把在前排就坐的高二代表队6人分别记为 ,现随机从中抽取2人上台抽奖,
,现随机从中抽取2人上台抽奖,
求 和
和 至少有一人上台抽奖的概率;
至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个 之间的均匀随机数
之间的均匀随机数 ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t该农产品.以X(单位: t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.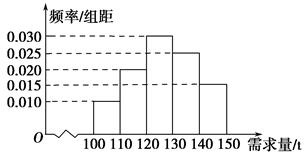
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率,求T的数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某工科院校对A,B两个专业的男女生人数进行调查,得到如下的列联表:
| | 专业A | 专业B | 总计 |
| 女生 | 12 | 4 | 16 |
| 男生 | 38 | 46 | 84 |
| 总计 | 50 | 50 | 100 |

| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目: 来源: 题型:解答题
设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和,求ξ的分布列;
(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若E(η)=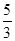 ,D(η)=
,D(η)=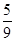 ,求a∶b∶c.
,求a∶b∶c.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com