
科目: 来源: 题型:解答题
某校为组建校篮球队,对报名同学进行定点投篮测试,规定每位同学最多投3次,每次在A或B处投篮,在A处投进一球得3分,在B处投进一球得2分,否则得0分,每次投篮结果相互独立,将得分逐次累加并用X表示,如果X的值不低于3分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮方案有以下两种:
方案1:先在A处投一球,以后都在B处投;
方案2:都在B处投篮.
已知甲同学在A处投篮的命中率为0.4,在B处投篮的命中率为0.6.
(1)甲同学若选择方案1,求X=2时的概率;
(2)甲同学若选择方案2,求X的分布列和数学期望;
(3)甲同学选择哪种方案通过测试的可能性更大?请说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5,4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(1)求取出的3个球编号都不相同的概率;
(2)记X为取出的3个球中编号的最小值,求X的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
为贯彻“激情工作,快乐生活”的理念,某单位在工作之余举行趣味知识有奖竞赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题的正确率为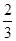 .
.
(1)求选手甲答题次数不超过4次可进入决赛的概率;
(2)设选手甲在初赛中答题的个数为X,试写出X的分布列,并求X的数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
市民李先生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机的.同一条道路去程与回程是否堵车相互独立.假设李先生早上需要先开车送小孩去丙地小学,再返回经甲地赶去乙地上班.假设道路A,B,D上下班时间往返出现拥堵的概率都是 ,道路C,E上下班时间往返出现拥堵的概率都是
,道路C,E上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
(1)求李先生的小孩按时到校的概率;
(2)李先生是否有七成把握能够按时上班?
(3)设X表示李先生下班时从单位乙到达小学丙遇到拥堵的次数,求X的均值.
查看答案和解析>>
科目: 来源: 题型:解答题
某学生参加某高校的自主招生考试,须依次参加A,B,C,D,E五项考试,如果前四项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试.已知每一项测试都是相互独立的,该生参加A,B,C,D四项考试不合格的概率均为 ,参加第五项不合格的概率为
,参加第五项不合格的概率为 .
.
(1)求该生被录取的概率;
(2)记该生参加考试的项数为X,求X的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙两人玩猜数字游戏,规则如下:
①连续竞猜3次,每次相互独立;
②每次竞猜时,先由甲写出一个数字,记为a,再由乙猜甲写的数字,记为b,已知a,b∈{0,1,2,3,4,5},若|a-b|≤1,则本次竞猜成功;
③在3次竞猜中,至少有2次竞猜成功,则两人获奖.
求甲乙两人玩此游戏获奖的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
为了解某班学生喜爱打篮球是否与性别有关,对本班48人进行了问卷调查得到了如下的2×2列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
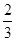 .
.| P(χ2≥x0)或 P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| x0(或k0) | 2.706 | 3.841 | 6.635 | 7.879 |
 ,其中n=n11+n12+n21+n22或K2=
,其中n=n11+n12+n21+n22或K2=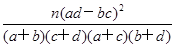 ,其中n=a+b+c+d)
,其中n=a+b+c+d)查看答案和解析>>
科目: 来源: 题型:解答题
袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子中随机抽取1个小球,取到标号为2的小球的概率是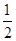 .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
| 品牌 | 甲 | 乙 | |||
| 首次出现故 障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
| 轿车数量(辆) | 2 | 3 | 45 | 5 | 45 |
| 每辆利润 (万元) | 1 | 2 | 3 | 1.8 | 2.9 |
查看答案和解析>>
科目: 来源: 题型:解答题
为备战2016年奥运会,甲、乙两位射击选手进行了强化训练.现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次,记录如下:
甲:8.3,9.0,7.9,7.8,9.4,8.9,8.4,8.3;
乙:9.2,9.5,8.0,7.5,8.2,8.1,9.0,8.5.
(1)画出甲、乙两位选手成绩的茎叶图;
(2)现要从中选派一人参加奥运会封闭集训,从统计学角度,你认为派哪位选手参加合理?简单说明理由;
(3)若将频率视为概率,对选手乙在今后的三次比赛成绩进行预测,记这三次成绩中不低于8.5分的次数为ξ,求ξ的分布列及均值E(ξ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com