
科目: 来源: 题型:解答题
如图,从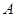 到
到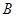 有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为
有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为 .
.
(1)当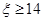 时,线路信息畅通,求线路信息畅通的概率;
时,线路信息畅通,求线路信息畅通的概率;
(2)求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
省少年篮球队要从甲、乙两所体校选拔队员。现将这两所体校共20名学生的身高绘制成如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.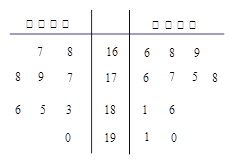
(1)用分层抽样的方法从“高个子”和“非高个子”中抽取5人,如果从这5人中随
机选2人,那么至少有一人是“高个子”的概率是多少?
(2)从两队的“高个子”中各随机抽取1人,求恰有1人身高达到190cm的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
省少年篮球队要从甲、乙两所体校选拔队员。现将这两所体校共20名学生的身高绘制成如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.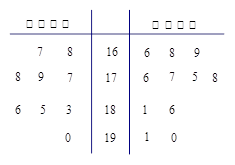
(Ⅰ)用分层抽样的方法从“高个子”和“非高个子”中抽取5人,如果从这5人中随机选2人,那么至少有一人是“高个子”的概率是多少?
(Ⅱ)若从所有“高个子”中随机选3名队员,用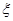 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出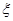 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某工厂三个车间共有工人1000人各车间男、女工人数如表:
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求x的值;
(2)现用分层抽样的方法在第一、第二、第三车间共抽取60名工人参加座谈分,问应在第三车间抽取多少名?
(3)已知y≥185,z≥185,求第三车间中女工比男工少的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目: 来源: 题型:解答题
对某校高一年级学生参加社区服务次数统计,随机抽取了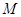 名学生作为样本,得到这
名学生作为样本,得到这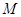 名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下: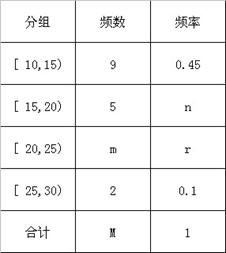
(1)求出表中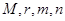 的值;
的值;
(2)在所取样本中,从参加社区服务的次数不少于 次的学生中任选
次的学生中任选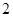 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间 内的概率.
内的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | 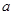 | 10 | 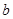 |
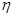 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.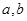 的值;
的值;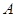 :“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率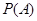 ;(3)求
;(3)求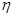 的分布列及数学期望
的分布列及数学期望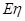 .
.查看答案和解析>>
科目: 来源: 题型:解答题
(14分)如图所示,机器人海宝按照以下程序运行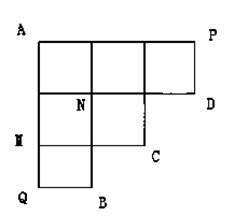
1从A出发到达点B或C或D,到达点B、C、D之一就停止;
②每次只向右或向下按路线运行;
③在每个路口向下的概率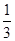 ;
;
④到达P时只向下,到达Q点只向右.
(1)求海宝过点从A经过M到点B的概率,求海宝过点从A经过N到点C的概率;
(2)记海宝到点B、C、D的事件分别记为X=1,X=2,X=3,求随机变量X的分布列及期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某社区举办防控甲型H7N9流感知识有奖问答比赛,甲、乙、丙三人同时回答一道卫生知识题,三人回答正确与错误互不影响。已知甲回答这题正确的概率是 ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是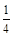 .
.
(I)求乙、丙两人各自回答这道题正确的概率;
(II)用 表示回答该题正确的人数,求
表示回答该题正确的人数,求 的分布列和数学期望
的分布列和数学期望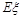 .
.
查看答案和解析>>
科目: 来源: 题型:解答题
小波以游戏方式决定参加学校合唱团还是参加学校排球队.游戏规则为:以O为起点,再从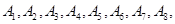 (如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为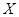 .若
.若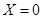 就参加学校合唱团,否则就参加学校排球队.
就参加学校合唱团,否则就参加学校排球队.
(I)求小波参加学校合唱团的概率;
(II)求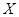 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com