
科目: 来源: 题型:解答题
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取的20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到频率分布表如下:

(1)求表中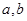 的值及分数在
的值及分数在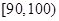 范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在
范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在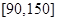 范围为及格);
范围为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
小明参加完高考后,某日路过一家电子游戏室,注意到一台电子游戏机的规则是:你可在1,2,3,4,5,6点中选一个,押上赌注a元。掷3枚骰子,如果所押的点数出现1次、2次、3次,那么原来的赌注仍还给你,并且你还分别可以收到赌注的1倍、2倍、3倍的奖励。如果所押的点数不出现,那么赌注就被庄家没收。
(1)求掷3枚骰子,至少出现1枚为1点的概率;
(2)如果小明准备尝试一次,请你计算一下他获利的期望值,并给小明一个正确的建议。
查看答案和解析>>
科目: 来源: 题型:解答题
一个盒子中装有分别标有数字1、2、3、4的4个大小、形状完全相同的小球,现从中有放回地随机抽取2个小球,抽取的球的编号分别记为 、
、 ,记
,记 .
.
(Ⅰ)求 取最大值的概率;
取最大值的概率;
(Ⅱ)求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为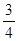 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为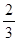 ,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分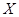 的分布列及数学期望
的分布列及数学期望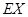 ;
;
查看答案和解析>>
科目: 来源: 题型:解答题
其市有小型超市72个,中型超市24个,大型超市12个,现采用分层抽样方法抽取9个超市对其销售商品质量进行调查.
(I)求应从小型、中型、大型超市分别抽取的个数;
(II)若从抽取的9个超市中随机抽取3个做进一步跟踪分析,记随机变量X为抽取的小型超市的个数,求随机变量X的分布列及数学期望E(X) .
查看答案和解析>>
科目: 来源: 题型:解答题
为了比较“传统式教学法”与我校所创立的“三步式教学法”的教学效果.共选100名学生随机分成两个班,每班50名学生,其中一班采取“传统式教学法”,二班实行“三步式教学法”
(Ⅰ)若全校共有学生2000名,其中男生1100名,现抽取100名学生对两种教学方式的受欢迎程度进行问卷调查,应抽取多少名女生?
(Ⅱ)下表1,2分别为实行“传统式教学”与“三步式教学”后的数学成绩:
表1
| 数学成绩 | 90分以下 | 90—120分 | 120—140分 | 140分以上 |
| 频 数 | 15 | 20 | 10 | 5 |
| 数学成绩 | 90分以下 | 90—120分 | 120—140分 | 140分以上 |
| 频 数 | 5 | 40 | 3 | 2 |
| 班 次 | 120分以下(人数) | 120分以上(人数) | 合计(人数) |
| 一班 | | | |
| 二班 | | | |
| 合计 | | | |
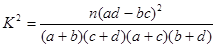 ,其中
,其中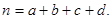
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是 ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
(Ⅰ)求乙得分的分布列和数学期望;
(Ⅱ)求甲、乙两人中至少有一人入选的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
一个袋子中装有6个红球和4个白球,假设每一个球被摸到的可能性是相等的.
(Ⅰ)从袋子中摸出3个球,求摸出的球为2个红球和1个白球的概率;
(Ⅱ)从袋子中摸出两个球,其中白球的个数为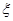 ,求
,求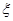 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
为了更好地开展社团活动,丰富同学们的课余生活,现用分层抽样的方法从“模拟联合国”,“街舞”,“动漫”,“话剧”四个社团中抽取若干人组成社团指导小组,有关数据见下表:(单位:人)
(1)求 的值;
的值;
(2)若从“动漫”与“话剧”社团已抽取的人中选2人担任指导小组组长,求这2人分别来自这两个社团的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名,以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”,求从这16人随机选取3人,至多有1人是“极幸福”的概率;
(2)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com