
科目: 来源: 题型:解答题
在一次购物抽奖活动中,假设某6张券中有一等奖 券1张,可获价值50元的奖品;有二等奖券1张,每张可获价值20元的奖品;其余4张没有奖.某顾客从此6张中任抽1张,求:
(1)该顾客中奖的概率;
(2)该顾客参加此活动可能获得的奖品价值的期望值.
查看答案和解析>>
科目: 来源: 题型:解答题
2013年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5浓度 (微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100) | 2 | 0.1 |
查看答案和解析>>
科目: 来源: 题型:解答题
为了响应学校“学科文化节”活动,数学组举办了一场数学知识比赛,共分为甲、乙两组.其中甲组得满分的有1个女生和3个男生,乙组得满分的有2个女生和4个男生.现从得满分的学生中,每组各任选2个学生,作为数学组的活动代言人.
(1)求选出的4个学生中恰有1个女生的概率;(2)设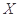 为选出的4个学生中女生的人数,求
为选出的4个学生中女生的人数,求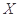 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
现有4个人去参加春节联欢活动,该活动有甲、乙两个项目可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个项目联欢,掷出点数为1或2的人去参加甲项目联欢,掷出点数大于2的人去参加乙项目联欢.
(Ⅰ)求这4个人中恰好有2人去参加甲项目联欢的概率;
(Ⅱ)求这4个人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数的概率;
(Ⅲ)用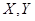 分别表示这4个人中去参加甲、乙项目联欢的人数,记
分别表示这4个人中去参加甲、乙项目联欢的人数,记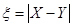 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望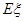 .
.
查看答案和解析>>
科目: 来源: 题型:解答题
从集合 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组 ,规定
,规定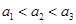
(1)从所有三元有序数组中任选一个,求它的所有元素之和等于10的概率;
(2)定义三元有序数组 的“项标距离”为
的“项标距离”为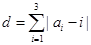 ,(其中
,(其中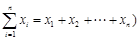 ,从所有三元有序数组中任选一个,求它的“项标距离”
,从所有三元有序数组中任选一个,求它的“项标距离”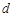 为偶数的概率;
为偶数的概率;
查看答案和解析>>
科目: 来源: 题型:解答题
某集团公司举办一次募捐爱心演出,有1000人参加,每人一张门票,每张100元。在演出过程中穿插抽奖活动,第一轮抽奖从这1000张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动。第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数 (
(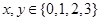 ),满足
),满足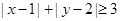 电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
(1)已知小明在第一轮抽奖中被抽中,求小明在第二轮抽奖中获奖的概率;
(2)若该集团公司望在此次活动中至少获得61875元的收益,则特等奖奖金最高可设置成多少元?
查看答案和解析>>
科目: 来源: 题型:解答题
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是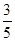 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是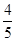 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用 表示张同学答对题的个数,求
表示张同学答对题的个数,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
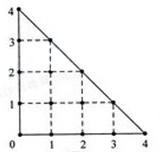
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横的交叉点记忆三角形的顶点)处都种了一株相同品种的作物。根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
查看答案和解析>>
科目: 来源: 题型:解答题
某车间共有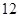 名工人,随机抽取
名工人,随机抽取 名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.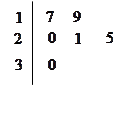
(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间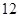 名工人中有几名优秀工人;
名工人中有几名优秀工人;
(Ⅲ) 从该车间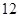 名工人中,任取
名工人中,任取 人,求恰有
人,求恰有 名优秀工人的概率.
名优秀工人的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过 小时收费
小时收费 元,超过
元,超过 小时的部分每小时收费
小时的部分每小时收费 元(不足
元(不足 小时的部分按
小时的部分按 小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过
小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过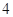 小时.
小时.
(1)若甲停车 小时以上且不超过
小时以上且不超过 小时的概率为
小时的概率为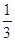 ,停车付费多于
,停车付费多于 元的概率为
元的概率为 ,求甲停车付费恰为
,求甲停车付费恰为 元的概率;
元的概率;
(2)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为 元的概率.
元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com