
科目: 来源: 题型:解答题
工商部门对甲、乙两家食品加工企业的产品进行深入检查后,决定对甲企业的5种产品和乙企业的3种产品做进一步的检验.检验员从以上8种产品中每次抽取一种逐一不重复地进行化验检验.
(1)求前3次检验的产品中至少1种是乙企业的产品的概率;
(2)记检验到第一种甲企业的产品时所检验的产品种数共为X,求X的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
口袋中有大小、质地均相同的7个球,3个红球,4个黑球,现在从中任取3个球。
(1)求取出的球颜色相同的概率;
(2)若取出的红球数设为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目: 来源: 题型:解答题
某广场上有4盏装饰灯,晚上每盏灯都随机地闪烁红灯或绿灯,每盏灯出现红灯的概率都是 ,出现绿灯的概率都是
,出现绿灯的概率都是 .记这4盏灯中出现红灯的数量为
.记这4盏灯中出现红灯的数量为 ,当这排装饰灯闪烁一次时:
,当这排装饰灯闪烁一次时:
(1)求 时的概率;(2)求
时的概率;(2)求 的数学期望.
的数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
现有甲、乙两个靶。某射手向甲靶射击一次,命中的概率为 ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。
,每命中一次得2分,没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。
(Ⅰ)求该射手恰好命中一次的概率;
(Ⅱ)求该射手的总得分X的分布列及数学期望EX.
查看答案和解析>>
科目: 来源: 题型:解答题
在一次购物抽奖活动中,假设某10张奖券中有一等奖卷1张,可获价值50元的奖品;有二等奖卷3张,每张可获价值10元的奖品;其余6张没有奖。某顾客从这10张中任抽2张,求:(1)该顾客中奖的概率;(2)该顾客获得的奖品总价值X(元)的分布列和数学期望。
查看答案和解析>>
科目: 来源: 题型:解答题
某工厂生产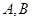 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
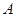 | 7 | 7 | 7.5 | 9 | 9.5 |
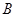 | 6 | 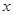 | 8.5 | 8.5 | 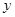 |
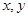 看不清,统计员只记得
看不清,统计员只记得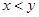 ,且
,且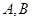 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.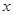 与
与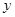 的值;
的值;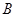 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率.查看答案和解析>>
科目: 来源: 题型:解答题
为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合 计 |
| 男 生 | | 6 | |
| 女 生 | 10 | | |
| 合 计 | | | 48 |
 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关? ,其中
,其中 
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:解答题
为提高学生的素质,学校决定开设一批选修课程,分别为“文学”、“艺术”、“竞赛”三类,这三类课程所含科目的个数分别占总数的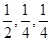 ,现有3名学生从中任选一个科目参加学习(互不影响),记
,现有3名学生从中任选一个科目参加学习(互不影响),记 为3人中选择的科目属于“文学”或“竞赛”的人数,求
为3人中选择的科目属于“文学”或“竞赛”的人数,求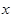 的分布列及期望。
的分布列及期望。
查看答案和解析>>
科目: 来源: 题型:解答题
为了保养汽车,维护汽车性能,汽车保养一般都在购车的4S店进行,某地大众汽车4S店售后服务部设有一个服务窗口专门接待保养预约。假设车主预约保养登记所需的时间互相独立,且都是整数分钟,对以往车主预约登记所需的时间统计结果如下:
| 登记所需时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
查看答案和解析>>
科目: 来源: 题型:解答题
一个盒子装有6张卡片,上面分别写着如下6个定义域为R的函数: ,
, ,
, ,
, ,
, ,
, .
.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得到一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com