
科目: 来源: 题型:解答题
某人上楼梯,每步上一阶的概率为 ,每步上二阶的概率为
,每步上二阶的概率为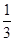 ,设该人从台阶下的平台开始出发,到达第
,设该人从台阶下的平台开始出发,到达第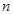 阶的概率为
阶的概率为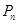 .
.
(1)求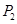 ;;
;;
(2)该人共走了5步,求该人这5步共上的阶数ξ的数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
一家化妆品公司于今年三八节期间在某社区举行了为期三天的“健康使用化妆品知识讲座”.每位社区居民可以在这三天中的任意一天参加任何一个讨论,也可以放弃任何一个讲座(规定:各个讲座达到预先设定的人数时称为满座).统计数据表明,各个讲座各天满座的概率如下表:
| | 洗发水讲座 | 洗面奶讲座 | 护肤霜讲座 | 活颜营养讲座 | 面膜使用讲座 |
| 3月8日 | 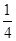 | 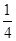 | 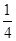 | 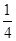 |  |
| 3月9日 |  |  |  |  | 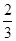 |
| 3月10日 | 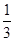 | 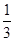 | 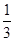 | 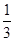 | 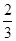 |
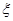 ,求随机变量
,求随机变量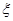 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目: 来源: 题型:解答题
为了解《中华人民共国道路交通安全法》在学生中的普及情况,调查部门对某学校6名学生进行问卷调查,6人得分情况如下:
5,6,7,8,9,10。
把这6名学生的得分看成一个总体。
(1)求该总体的平均数;
(2)求该总体的的方差;
(3)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本,求该样本平均数于总体平均数之差的绝对值不超过0.5的概率。
查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为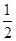 和
和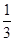 , 求:
, 求:
(1)甲、乙两人至少有一个人破译出密码的概率;
(2)两人都没有破译出密码的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
某射手在一次射击中射中10环、9环、8环、7环, 7环以下的概率
分别为0.24,0.28,0.19,0.16,0.13,计算这个射手在一次射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不是8环的概率。
查看答案和解析>>
科目: 来源: 题型:解答题
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在
下落的过程中,将3次遇到黑色障碍物,最后落入 袋或
袋或 袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是 .
.
(Ⅰ)求小球落入 袋中的概率
袋中的概率 ;
;
(Ⅱ)在容器入口处依次放入4个小球,记 为落入
为落入 袋中的小球个数,试求
袋中的小球个数,试求 的概率和
的概率和 的数学期望
的数学期望 .
.
查看答案和解析>>
科目: 来源: 题型:解答题
为了防止受到核污染的产品影响我国民众的身体健康,要求产品进入市场前必须进行两轮核放射检测,只有两轮都合格才能进行销售。已知某产品第一轮检测不合格的概率为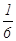 ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为 ,两轮检测是否合格相互没有影响。
,两轮检测是否合格相互没有影响。
(1)求该产品不能销售的概率
(2)如果产品可以销售,则每件产品可获利40元;如果产品不能销售,则每件产品亏损80元(即获利-80元)。已知一箱中有4件产品,记可销售的产品数为X,求X的分布列,并求一箱产品获利的均值。
查看答案和解析>>
科目: 来源: 题型:解答题
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
| 日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 (°C) (°C) | 10 | 11 | 13 | 12 | 8 |
发芽数 (颗) (颗) | 23 | 25 | 30 | 26 | 16 |
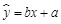 已知回归直线方程是:
已知回归直线方程是: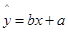 ,其中
,其中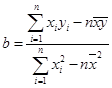 ,
, ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com