
科目: 来源: 题型:解答题
为了参加 贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出
贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
| 班级 | 高三(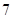 )班 )班 | 高三(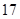 )班 )班 | 高二(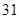 )班 )班 | 高二(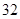 )班 )班 |
| 人数 | 12 | 6 | 9 | 9 |
查看答案和解析>>
科目: 来源: 题型:解答题
2011年4月28日世界园艺博览会将在陕西西安浐灞生态区举行,为了接待来自国内外的各界人士,需招募一批志愿者,要求志愿者不仅要有一定的气质,还需有丰富的人文、地理、历史等文化知识。志愿者的选拔分面试和知识问答两场,先是面试,面试通过后每人积60分,然后进入知识问答。知识问答有A,B,C,D四个题目,答题者必须按A,B,C,D顺序依次进行,答对A,B,C,D四题分别得20分、20分、40分、60分,每答错一道题扣20分,总得分在面试60分的基础上加或减。答题时每人总分达到100分或100分以上,直接录用不再继续答题;当四道题答完总分不足100分时不予录用。
假设志愿者甲面试已通过且第二轮对A,B,C,D四个题回答正确的概率依次是 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.
(Ⅰ) 用X表示志愿者甲在知识问答结束时答题的个数,求X的分布列和数学期望;
(Ⅱ)求志愿者甲能被录用的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
袋子里有大小相同但标有不同号码的3个红球和4个黑球,从袋子里随机取出4个球.
⑴求取出的红球数?的概率分布列;
⑵若取到每个红球得2分,取到每个黑球得1分,求得分不超过5分的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
某商场为吸引顾客消费推出一项优惠活动,活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在 区域返券60元;停在
区域返券60元;停在 区域返券30元;停在
区域返券30元;停在 区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为 (元),求随机变量
(元),求随机变量 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某某种饮料每箱6听,如果其中有两听不合格产品.
(1)质检人员从中随机抽出1听,检测出不合格的概率多大?;
(2)质检人员从中随机抽出2听,设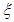 为检测出不合格产品的听数,求
为检测出不合格产品的听数,求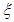 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某学生参加某高校的自主招生考试,须依次参加A、B、C、D、E五项考试,如果前四项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试。已知每一项测试都是相互独立的,该生参加A、B、C、D四项考试不合格的概率均为 ,参加第五项不合格的概率为
,参加第五项不合格的概率为
(1)求该生被录取的概率;
(2)记该生参加考试的项数为 ,求
,求 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:解答题
(1)甲盒中有红,黑,白三种颜色的球各3个,乙盒子中有黄,黑,白三种颜色的球各2个,从两个盒子中各取1个球,求取出的两个球是不同颜色的概率。
(2)在单位圆的圆周上随机取三点A、B、C,求 是锐角三角形的概率。
是锐角三角形的概率。
查看答案和解析>>
科目: 来源: 题型:解答题
一个袋中装有大小相同的黑球和白球共9个,从中任取3个球,记随机变量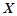 为取出3球中白球的个数,已知
为取出3球中白球的个数,已知 .
.
(Ⅰ)求袋中白球的个数;
(Ⅱ)求随机变量 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某商场共五层,从五层下到四层有3个出口,从三层下到二层有4个出口,从二层下到一层有4个出口,从一层走出商场有6个出口。安全部门在每层安排了一名警员值班,负责该层的安保工作。假设每名警员到该层各出口处的时间相等,某罪犯在五楼犯案后,欲逃出商场,各警员同时接到指令,选择一个出口进行围堵。逃犯在每层选择出口是等可能的。已知他被三楼警员抓获的概率为 。
。
(Ⅰ)问四层下到三层有几个出口?
(Ⅱ)天网恢恢,疏而不漏,犯罪嫌疑人最终落入法网。设抓到逃犯时,他已下了 层楼,写出
层楼,写出 的分布列,并求
的分布列,并求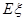 。
。
查看答案和解析>>
科目: 来源: 题型:解答题
小王参加一次比赛,比赛共设三关,第一、二关各有两个必答题,如果每关两个问题都答对,可进入下一关,第三关有三个问题,只要答对其中两个问题,则闯关成功.每过一关可一次性获得价值分别为1000元,3000元,6000元的奖品(不重复得奖),小王对三关中每个问题回答正确的概率依次为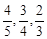 ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.
(1)求小王过第一关但未过第二关的概率;
(2)用X表示小王所获得奖品的价值,写出X的概率分布列,并求X的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com