
科目: 来源: 题型:解答题
如下图,用A、B、C三类不同的元件连接两个系统N1,N2,当元件A、B、C都正常工作时系统N1正常工作,当元件A正常工作且元件B、C至少有一个正常工作时系统N2正常工作,已知元件A、B、C正常工作的概率分别为0.80,0.90,0.90,分别求系统N1,N2正常工作的概率p1,p2.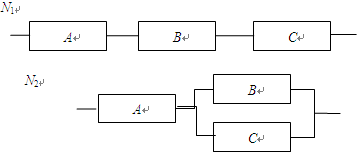
查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率为
,乙每次击中目标的概率为 ,两人间每次射击是否击中目标互不影响。
,两人间每次射击是否击中目标互不影响。
(1)求乙至多击中目标2次的概率;
(2)求甲恰好比乙多击中目标1次的概率。
查看答案和解析>>
科目: 来源: 题型:解答题
有20件产品,其中5件是次品,其余都是合格品,现不放回的从中依次抽2件.求:⑴第一次抽到次品的概率;⑵第一次和第二次都抽到次品的概率;⑶在第一次抽到次品的条件下,第二次抽到次品的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
(本小题满分12分)
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球中恰有1个红球的概率;
(Ⅱ)设“从甲盒内取出的2个球恰有1个为黑球”为事件A;“从乙盒内取出的2个球都是黑球”为事件B,求在事件A发生的条件下,事件B发生的概率;
(Ⅲ)设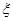 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求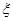 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目: 来源: 题型:解答题
(本小题满分12分)某班从6名班干部中(男生4人,女生2人)选3人参加学校义务劳动;(1)求男生甲或女生乙被选中的概率;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率;
(3)设所选3人中女生人数为 ,求
,求 的分布列及数学期望。
的分布列及数学期望。
查看答案和解析>>
科目: 来源: 题型:解答题
(本题满分12分)一厂家向用户提供的一箱产品共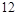 件,其中有
件,其中有 件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(Ⅰ)求这箱产品被用户接收的概率;
(Ⅱ)记抽检的产品件数为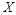 ,求随机变量
,求随机变量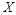 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
甲打靶射击,有4发子弹,其中有一发是空弹(“空弹”即只有弹体没有弹头的子弹).
(1)如果甲只射击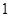 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;
(2)如果甲共射击 次,求在这三枪中出现空弹的概率
次,求在这三枪中出现空弹的概率
查看答案和解析>>
科目: 来源: 题型:解答题
甲设计了一个摸奖游戏,在一个口袋中装有同样大小的10个球,分别标有数字0,1,2,……9这十个数字,摸奖者交5元钱可参加一回摸球活动,一回摸球活动的规则是:摸奖者在摸球前先随机确定(预报)3个数字,然后开始在袋中不放回地摸3次球,每次摸一个,摸得3个球的数字与预先所报数字均不相同的奖1元,有1个数字相同的奖2元,2个数字相同的奖10元,3个数字相同的奖50元,设ξ为摸奖者一回所得奖金数,求ξ的分布列和摸奖人获利的数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
一个口袋中有红球3个,白球4个.
(Ⅰ)从中不放回地摸球,每次摸2个,摸到的2个球中至少有1个红球则中奖,求恰好第2次中奖的概率;
(Ⅱ)从中有放回地摸球,每次摸2个,摸到的2个球中至少有1个红球则中奖,连续摸4次,求中奖次数X的数学期望E(X).
查看答案和解析>>
科目: 来源: 题型:解答题
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中的微量元素 ,
, 的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
 | 160 | 178 | 166 | 175 | 180 |
 | 75 | 80 | 77 | 70 | 81 |
 且
且 为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数
为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com