
科目: 来源: 题型:解答题
本小题满分12分)奇瑞公司生产的“奇瑞”轿车是我国民族品牌.该公司2009年生产的“旗云”、“风云”、“ ”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:
”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:
| 车型 | 旗云 | 风云 |  |
| 舒适 | 100 | 150 |  |
| 标准 | 300 |  | 600 |
 、
、 的值;
的值; ”轿车,该销售公司又从中随机抽取了2辆作为奖品回馈消费者.求至少有一辆是舒适型轿车的概率.
”轿车,该销售公司又从中随机抽取了2辆作为奖品回馈消费者.求至少有一辆是舒适型轿车的概率.查看答案和解析>>
科目: 来源: 题型:解答题
某校教务处要对高三上学期期中数学试卷进行调研,考察试卷中某道填空题的得分情况.已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从该校1468份试卷中随机抽取1000份试卷,其中该题的得分组成容量为1000的样本,统计结果如下表:
| 第一空得分情况 | | 第二空得分情况 | ||||
| 得分 | 0 | 3 | | 得分 | 0 | 2 |
| 人数 | 198 | 802 | | 人数 | 698 | 302 |
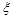 的数学期望.
的数学期望.查看答案和解析>>
科目: 来源: 题型:解答题
广雅中学在高二年级开设了 ,
, ,
, 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从
三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从 ,
, ,
, 三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
| 兴趣小组 | 小组人数 | 抽取人数 |
 | 24 |  |
 | 36 | 3 |
 | 48 |  |
 ,
, 的值;
的值; ,
, 两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自兴趣小组
两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自兴趣小组 的概率.
的概率.查看答案和解析>>
科目: 来源: 题型:解答题
本小题满分13分)
先后随机投掷2枚正方体(六面分别标有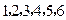 )骰子,其中
)骰子,其中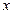 表示第
表示第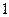 枚骰子出现的点数,
枚骰子出现的点数,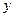 表示第
表示第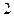 枚骰子出现的点数。
枚骰子出现的点数。
(1)求点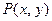 在直线
在直线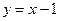 上的概率;
上的概率;
(2)求点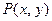 满足
满足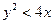 的概率。
的概率。
查看答案和解析>>
科目: 来源: 题型:解答题
(本题满分14分)从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同.
(Ⅰ)若抽取后又放回,抽取3次,求恰好抽到2次为红球的概率;
(Ⅱ)若抽取后不放回,设抽完红球所需的次数为 ,求
,求 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目: 来源: 题型:解答题
(本小题满分l2分)
在“环境保护低碳生活知识竞赛”第一环节测试中,设有A、B、C三道必答题,分值依次为20分、30分、50分.竞赛规定:若参赛选手连续两道题答题错误,则必答题总分记为零分;否则各题得分之和记为必答题总分.已知某选手回答A、B、C三道题正确的概率分别为 、
、 、
、 ,且回答各题时相互之间没有影响.
,且回答各题时相互之间没有影响.
(1) 若此选手可以自由选择答题顺序,求其必答题总分为50分的概率;
(2) 若此选手按A、B、C的顺序答题,求其必答题总分 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
( 12分)
甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是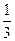 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数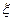 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com