
科目: 来源: 题型:填空题
对于问题:“已知关于 的不等式
的不等式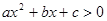 的解集为(-1,2),解关于
的解集为(-1,2),解关于 的不等式
的不等式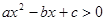 ”,给出如下一种解法:
”,给出如下一种解法:
解:由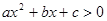 的解集为(-1,2),得
的解集为(-1,2),得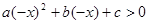 的解集为(-2,1),
的解集为(-2,1),
即关于 的不等式
的不等式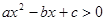 的解集为(-2,1)
的解集为(-2,1)
参考上述解法,若关于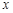 的不等式
的不等式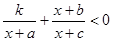 的解集为(-1,
的解集为(-1, 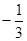 )
)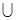 (
( ,1),则关于
,1),则关于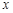 的不等式
的不等式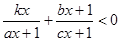 的解集为________________
的解集为________________
查看答案和解析>>
科目: 来源: 题型:填空题
将长度为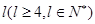 的线段分成
的线段分成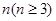 段,每段长度均为正整数,并要求这
段,每段长度均为正整数,并要求这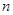 段中的任意三段都不能构成三角形.例如,当
段中的任意三段都不能构成三角形.例如,当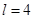 时,只可以分为长度分别为1,1,2的三段,此时
时,只可以分为长度分别为1,1,2的三段,此时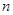 的最大值为3;当
的最大值为3;当 时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时
时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时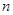 的最大值为4.则:
的最大值为4.则:
(1)当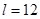 时,
时,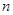 的最大值为________;
的最大值为________;
(2)当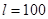 时,
时,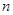 的最大值为________.
的最大值为________.
查看答案和解析>>
科目: 来源: 题型:填空题
将长度为 的线段分成
的线段分成 段,每段长度均为正整数,并要求这
段,每段长度均为正整数,并要求这 段中的任意三段都不能构成三角形.例如,当
段中的任意三段都不能构成三角形.例如,当 时,只可以分为长度分别为1,1,2的三段,此时
时,只可以分为长度分别为1,1,2的三段,此时 的最大值为3;当
的最大值为3;当 时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时
时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时 的最大值为4.则:
的最大值为4.则:
(1)当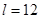 时,
时, 的最大值为________;(2)当
的最大值为________;(2)当 时,
时, 的最大值为________.
的最大值为________.
查看答案和解析>>
科目: 来源: 题型:填空题
在平面几何中有如下结论:若正三角形ABC的内切圆面积为 ,外接圆面积为
,外接圆面积为 ,则
,则 .推广到空间几何体中可以得到类似结论:若正四面体ABCD的内切球体积为
.推广到空间几何体中可以得到类似结论:若正四面体ABCD的内切球体积为 ,外接球体积为
,外接球体积为 ,则
,则 =___________.
=___________.
查看答案和解析>>
科目: 来源: 题型:填空题
(2013•湖北)古希腊毕达哥拉斯学派的数学家研究过各种多边形数,如三角形数1,3,6,10,…,第n个三角形数为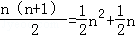 .记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:
.记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:
三角形数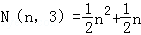 ,
,
正方形数N(n,4)=n2,
五边形数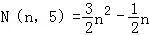 ,
,
六边形数N(n,6)=2n2﹣n,
…
可以推测N(n,k)的表达式,由此计算N(10,24)= _________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com