
科目: 来源:不详 题型:单选题
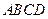 --
--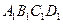 ,E、F分别是
,E、F分别是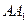 、
、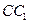 的中点,p是
的中点,p是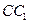 上的动点(包括端点),过E、D、P作正方体的截面,若截面为四边形,则P的轨迹是
上的动点(包括端点),过E、D、P作正方体的截面,若截面为四边形,则P的轨迹是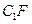 B、线段
B、线段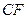 C、线段
C、线段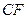 和一点
和一点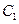 D、线段
D、线段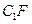 和一点C。
和一点C。查看答案和解析>>
科目: 来源:不详 题型:填空题
查看答案和解析>>
科目: 来源:不详 题型:解答题
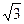 的菱形,∠BAD=60°,侧面VAD⊥底面ABCD,VA=VD,E为AD的中点.
的菱形,∠BAD=60°,侧面VAD⊥底面ABCD,VA=VD,E为AD的中点.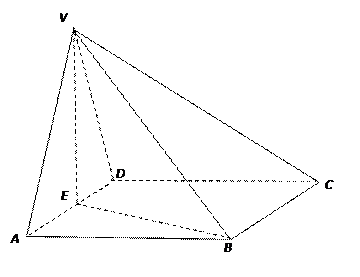 |
查看答案和解析>>
科目: 来源:不详 题型:填空题
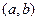 为圆心,以
为圆心,以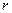 为半径的圆的方程为
为半径的圆的方程为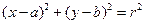 ,类似的在空间以点
,类似的在空间以点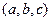 为球心,以
为球心,以 为半径的球面方程为 .
为半径的球面方程为 .查看答案和解析>>
科目: 来源:不详 题型:解答题
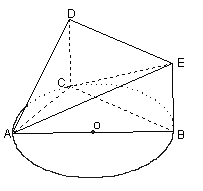
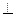 平面ABC ,
平面ABC ,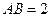 ,
,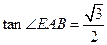 .
.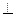 平面
平面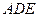 ;
;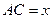 ,
,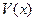 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求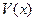 的表达式;
的表达式;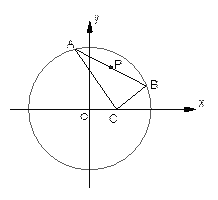
 (3)当
(3)当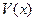 取得最大值时,求证:AD=CE.
取得最大值时,求证:AD=CE.查看答案和解析>>
科目: 来源:不详 题型:解答题
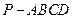 的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.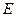 是侧棱
是侧棱 上的动点.
上的动点.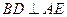
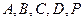 在同一球面上,求该球的体积.
在同一球面上,求该球的体积. | |||
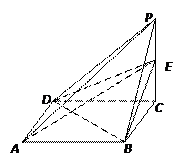 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com