
科目: 来源:不详 题型:单选题
零件数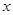 (个) (个) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
加工时间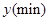 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 |
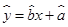 ,则点
,则点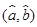 在直线
在直线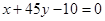 的( )
的( )查看答案和解析>>
科目: 来源:不详 题型:单选题
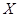 与
与 是否有关系时,通过查阅下表来确定“
是否有关系时,通过查阅下表来确定“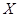 和
和 有关系”的可信度。如果
有关系”的可信度。如果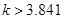 ,那么就有把握认为“
,那么就有把握认为“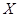 和
和 有关系”的百分比为( )
有关系”的百分比为( ) |  |  |  |  |  |  |  |  |  |  |
 |  |  | 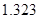 |  |  |  |  |  |  |  |
查看答案和解析>>
科目: 来源:不详 题型:解答题
| | 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |

 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源:不详 题型:解答题
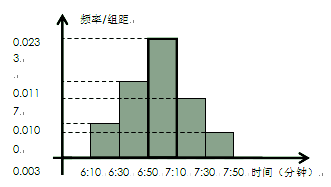
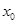 ;
;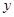 在上午
在上午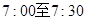 之间,而送报人每天在
之间,而送报人每天在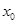 时刻前后
时刻前后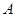 )的概率;
)的概率;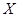 的数学期望.
的数学期望.查看答案和解析>>
科目: 来源:不详 题型:解答题
 小于
小于 为二等品,小于
为二等品,小于 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:| 测试指标 |  |  |  |  |  |  |
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
查看答案和解析>>
科目: 来源:不详 题型:单选题
 ,
, ”是“(x0,y0)满足线性回归方程y=bx+a”的( )
”是“(x0,y0)满足线性回归方程y=bx+a”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目: 来源:不详 题型:解答题
| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
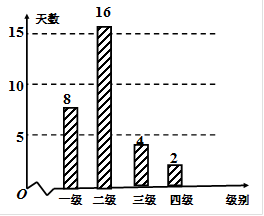
查看答案和解析>>
科目: 来源:不详 题型:解答题

查看答案和解析>>
科目: 来源:不详 题型:解答题
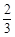 ,求甲在初赛中答题个数的分布列和数学期望.
,求甲在初赛中答题个数的分布列和数学期望.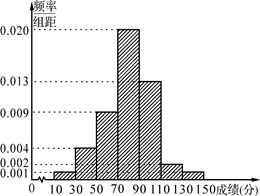
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com