
科目: 来源:不详 题型:解答题
| 年份 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 |
| x(kg) | 70 | 74 | 80 | 78 | 85 | 92 | 90 | 95 |
| y(t) | 5.1 | 6.0 | 6.8 | 7.8 | 9.0 | 10.2 | 10.0 | 12.0 |
| | ||||||||
| 年份 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | |
| x(kg) | 92 | 108 | 115 | 123 | 130 | 138 | 145 | |
| y(t) | 11.5 | 11.0 | 11.8 | 12.2 | 12.5 | 12.8 | 13.0 | |
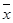 =101,
=101,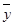 ≈10.113 3,
≈10.113 3,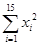 =161 125,
=161 125,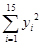 =1 628.55,
=1 628.55,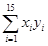 =16 076.8)
=16 076.8)查看答案和解析>>
科目: 来源:不详 题型:解答题
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.9830.02), | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.9830.02), | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| | 甲厂 | 乙厂 | 合计 |
| 优质品 | | | |
| 非优质品 | | | |
| 合 计 | | | |
| P(χ2≥x0) | 0.05 | 0.01 |
| x0 | 3.841 | 6.635 |
查看答案和解析>>
科目: 来源:不详 题型:解答题
| x | 35 | 40 | 45 | 50 |
| y | 56 | 41 | 28 | 11 |
查看答案和解析>>
科目: 来源:不详 题型:解答题
| 年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 91.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| | |||||||
| 年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
查看答案和解析>>
科目: 来源:不详 题型:解答题
 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为 ,
, ,
, ,
, ,由此得到样本的重量频率分布直方图,如图
,由此得到样本的重量频率分布直方图,如图
 的值;
的值; 组的频率为
组的频率为 ,第
,第 组区间的中点值为
组区间的中点值为 ,则样本数据的平均值为
,则样本数据的平均值为 .)
.) 个小球,其中重量在
个小球,其中重量在 内的小球个数为
内的小球个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目: 来源:不详 题型:解答题
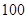 名高一新生分成水平相同的甲、乙两个“平行班”,每班
名高一新生分成水平相同的甲、乙两个“平行班”,每班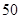 人,吴老师采用
人,吴老师采用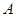 、
、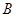 两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取
两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取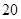 名学生的成绩进行统计,作出的茎叶图如下:
名学生的成绩进行统计,作出的茎叶图如下: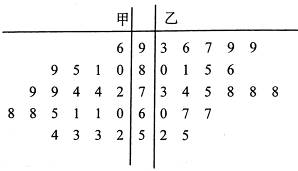
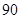 分者为“成绩优秀”.
分者为“成绩优秀”.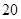 个个体中,从不低于
个个体中,从不低于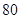 分的成绩中随机抽取
分的成绩中随机抽取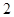 个,记随机变量
个,记随机变量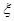 为抽到“成绩优秀”的个数,求
为抽到“成绩优秀”的个数,求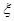 的分布列及数学期望
的分布列及数学期望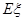 ;
;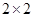 列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?| | 甲班(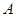 方式) 方式) | 乙班(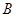 方式) 方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |
查看答案和解析>>
科目: 来源:不详 题型:解答题
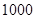 人,其中
人,其中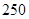 名工人参加过短期培训(称为
名工人参加过短期培训(称为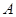 类工人),另外
类工人),另外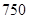 名工人参加过长期培训(称为
名工人参加过长期培训(称为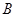 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按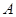 类、
类、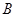 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查  名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).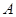 类工人和
类工人和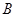 类工人中各抽查多少工人?
类工人中各抽查多少工人?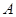 类工人中的抽查结果和从
类工人中的抽查结果和从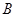 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.| 生产能力分组 | 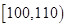 | 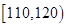 | 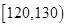 | 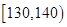 | 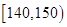 |
| 人数 | 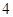 | 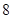 | 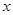 | 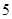 | 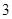 |
| 生产能力分组 | 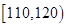 | 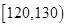 | 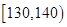 | 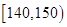 |
| 人数 | 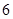 | 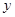 | 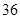 | 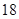 |
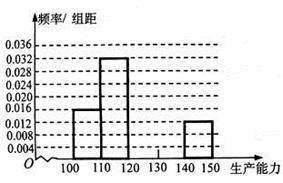
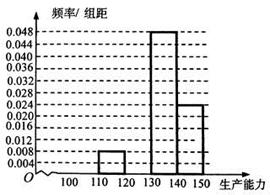
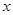 、
、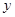 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图;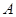 类工人和
类工人和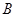 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组查看答案和解析>>
科目: 来源:不详 题型:单选题
| 气温x(°C) | 18 | 13 | 10 | -1 |
| 山高y(km) | 24 | 34 | 38 | 64 |
 ,由此请估计出山高为72(km)处气温的度数为( )
,由此请估计出山高为72(km)处气温的度数为( )查看答案和解析>>
科目: 来源:不详 题型:解答题

查看答案和解析>>
科目: 来源:不详 题型:填空题
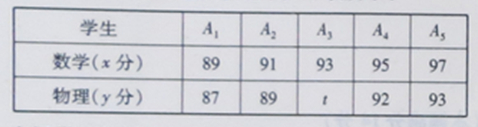
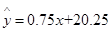 ,那么表中t的值为 .
,那么表中t的值为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com