
科目: 来源:不详 题型:单选题
 名学生学习数学与学习物理的成绩进行调查,得到如下表所示:
名学生学习数学与学习物理的成绩进行调查,得到如下表所示:| | 数学成绩较好 | 数学成绩一般 | 合计 |
| 物理成绩较好 | 18 | 7 | 25 |
| 物理成绩一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
 ,解得
,解得
 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
 的前提下,认为“数学成绩与物理成绩有关”
的前提下,认为“数学成绩与物理成绩有关” 的前提下,认为“数学成绩与物理成绩无关”
的前提下,认为“数学成绩与物理成绩无关” 的把握认为“数学成绩与物理成绩有关”
的把握认为“数学成绩与物理成绩有关” 以上的把握认为“数学成绩与物理成绩无关”
以上的把握认为“数学成绩与物理成绩无关”查看答案和解析>>
科目: 来源:不详 题型:解答题
 有关.
有关.  是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.  日均值越小,空气质量越好. 2012年2月29日,国家环保部发布的《环境空气质量标准》见下表:
日均值越小,空气质量越好. 2012年2月29日,国家环保部发布的《环境空气质量标准》见下表:  日均值k(微克) 日均值k(微克) | 空气质量等级 |
 | 一级 |
 | 二级 |
 | 超标 |
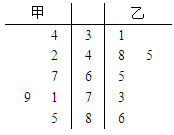
 日均值作为样本,样本数据茎叶图如上右图所示(十位为茎,个位为叶). (Ⅰ)分别求出甲、乙两市
日均值作为样本,样本数据茎叶图如上右图所示(十位为茎,个位为叶). (Ⅰ)分别求出甲、乙两市 日均值的样本平均数,并由此判断哪个市的空气质量较好;
日均值的样本平均数,并由此判断哪个市的空气质量较好;查看答案和解析>>
科目: 来源:不详 题型:解答题
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ▓ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| | 合计 | ▓ | ▓ |
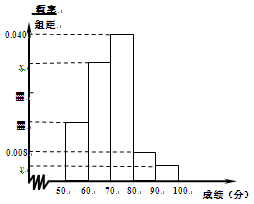
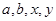 的值;
的值;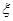 表示所抽取的2名同学中来自第5组的人数,求
表示所抽取的2名同学中来自第5组的人数,求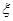 的分布列及其数学期望.
的分布列及其数学期望.查看答案和解析>>
科目: 来源:不详 题型:单选题
 产品过程中记录的产品
产品过程中记录的产品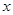 (吨)与相应的生产能耗
(吨)与相应的生产能耗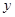 (吨)的几组对应数据,根据表中提供的数据,求出
(吨)的几组对应数据,根据表中提供的数据,求出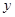 关于
关于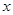 的线性回归方程为
的线性回归方程为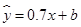 ,那么
,那么 的值为( )
的值为( )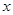 | 3 | 4 | 5 | 6 |
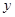 | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目: 来源:不详 题型:单选题

| A.117 | B.118 | C.118.5 | D.119.5 |
查看答案和解析>>
科目: 来源:不详 题型:单选题


 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
)查看答案和解析>>
科目: 来源:不详 题型:解答题
| 编号 | 性别 | 投篮成绩 |
| 2 | 男 | 90 |
| 7 | 女 | 60 |
| 12 | 男 | 75 |
| 17 | 男 | 80 |
| 22 | 女 | 83 |
| 27 | 男 | 85 |
| 32 | 女 | 75 |
| 37 | 男 | 80 |
| 42 | 女 | 70 |
| 47 | 女 | 60 |
| 编号 | 性别 | 投篮成绩 |
| 1 | 男 | 95 |
| 8 | 男 | 85 |
| 10 | 男 | 85 |
| 20 | 男 | 70 |
| 23 | 男 | 70 |
| 28 | 男 | 80 |
| 33 | 女 | 60 |
| 35 | 女 | 65 |
| 43 | 女 | 70 |
| 48 | 女 | 60 |
| | 优秀 | 非优秀 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | 10 |
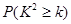 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
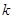 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
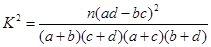 ,其中
,其中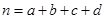 )
)查看答案和解析>>
科目: 来源:不详 题型:解答题
 ,第二类在
,第二类在 ,第三类在
,第三类在 (单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示. 
 为获奖户数,求
为获奖户数,求 的数学期望
的数学期望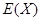 与方差
与方差 .
.查看答案和解析>>
科目: 来源:不详 题型:解答题
 人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图: ,求
,求 的分布列和期望
的分布列和期望 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com