
科目: 来源:不详 题型:单选题
| A.身高一定是145.83cm | B.身高在145.83cm以上 |
| C.身高在145.83cm以下 | D.身高在145.83cm左右 |
查看答案和解析>>
科目: 来源:不详 题型:解答题
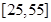 岁的人群随机抽取
岁的人群随机抽取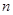 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
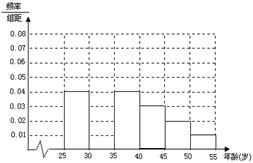
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图: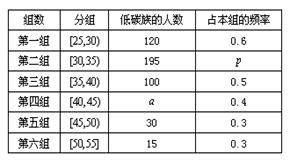
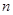 、
、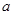 、
、 的值;
的值;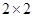 维列表,并判断能否有99.9%的把握认定该地区的生活习惯是否符合低碳观念与人的年龄有关?
维列表,并判断能否有99.9%的把握认定该地区的生活习惯是否符合低碳观念与人的年龄有关?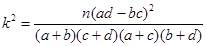
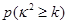 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
是否低碳族  年龄组 年龄组 | 青年 | 老年 |
| 低碳族 | | |
| 非低碳族 | | |
查看答案和解析>>
科目: 来源:不详 题型:解答题
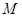 名学生作为样本,得到这
名学生作为样本,得到这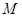 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下: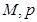 及图中
及图中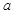 的值;
的值;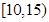 内的人数;
内的人数;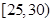 内的概率.
内的概率.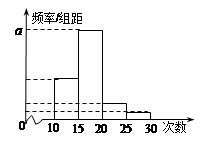
| 分组 | 频数 | 频率 |
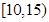 | 10 | 0.25 |
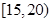 | 24 | 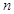 |
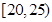 | 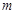 | 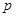 |
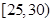 | 2 | 0.05 |
| 合计 | 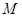 | 1 |
查看答案和解析>>
科目: 来源:不详 题型:填空题
 (单位:百元)与当天平均气温
(单位:百元)与当天平均气温 (单位:
(单位: )之间的关系如下:
)之间的关系如下:  | -2 | -1 | 0 | 1 | 2 |
 | 5 | 4 | 2 | 2 | 1 |
 与
与 之间的三个线性回归方程(1)
之间的三个线性回归方程(1) (2)
(2) (3)
(3) ,其中正确的是________________(填写序号)
,其中正确的是________________(填写序号)查看答案和解析>>
科目: 来源:不详 题型:解答题

查看答案和解析>>
科目: 来源:不详 题型:解答题


 的分布列和数学期望;
的分布列和数学期望;

查看答案和解析>>
科目: 来源:不详 题型:解答题
 表示.
表示. 的值;
的值; ,求随机变量
,求随机变量 的分布列和均值(数学期望).
的分布列和均值(数学期望).
查看答案和解析>>
科目: 来源:不详 题型:解答题
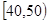 ,
,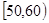 ,…,
,…,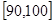 后得到如图4的频率分布直方图.
后得到如图4的频率分布直方图.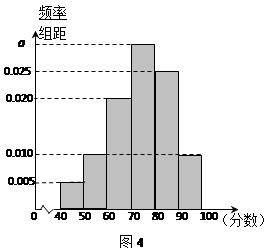
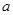 的值;
的值; 与
与 两个分数段内的学
两个分数段内的学查看答案和解析>>
科目: 来源:不详 题型:解答题
 ,A、B在MN上的射影P、Q之间距离为12km,现计划修普通公路把这两个城镇与高速公路相连接,若普通公路造价为50万元/km;而每个与高速公路连接的立交出入口修建费用为200万元。设计部门提交了以下三种修路方案:
,A、B在MN上的射影P、Q之间距离为12km,现计划修普通公路把这两个城镇与高速公路相连接,若普通公路造价为50万元/km;而每个与高速公路连接的立交出入口修建费用为200万元。设计部门提交了以下三种修路方案:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com