
科目: 来源:不详 题型:单选题
A.回归直线必过样本中心点 |
| B.回归直线就是散点图中经过样本数据点最多的那条直线 |
| C.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么此人有99%的可能患有肺病 |
| D.某车间包装一种产品,在自动包装的传送带上每隔30分钟抽取一件产品作检验,这种抽样为简单随机抽样 |
查看答案和解析>>
科目: 来源:不详 题型:单选题
| A.某车间包装一种产品,在自动包装的传送带上每隔30分钟抽取一件产品作检验,这种抽样为系统抽样 |
| B.回归直线就是散点图中经过样本数据点最多的那条直线 |
| C.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么此人有99%的可能患有肺病 |
D.设X服从正态分布 ,若X在(0,2)内取值的概率为0.4,则X在 ,若X在(0,2)内取值的概率为0.4,则X在 内取值的概率为0.6 内取值的概率为0.6 |
查看答案和解析>>
科目: 来源:不详 题型:解答题
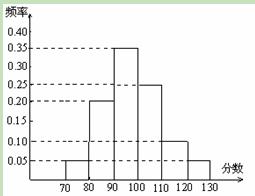
查看答案和解析>>
科目: 来源:不详 题型:解答题

查看答案和解析>>
科目: 来源:不详 题型:解答题
 带来的便捷与舒适的同时,却不得不呼吸汽车排放的尾气”,汽车已是城市中碳排放量比较大的行业之一.某市为响应国家节能减排,更好地保护环境,决定将于
带来的便捷与舒适的同时,却不得不呼吸汽车排放的尾气”,汽车已是城市中碳排放量比较大的行业之一.某市为响应国家节能减排,更好地保护环境,决定将于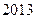 年起取消
年起取消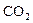 排放量超过
排放量超过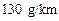 的
的 型新车挂牌.检测单位对目前该市保有量最大的甲类
型新车挂牌.检测单位对目前该市保有量最大的甲类 型品牌车随机抽取
型品牌车随机抽取 辆进行了
辆进行了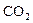 排放量检测,
排放量检测, 记录如下(单位:
记录如下(单位: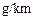 ).
).
 ,求
,求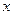 的值及样本标准差;
的值及样本标准差;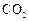 排放量的概率是多少?
排放量的概率是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com