
科目: 来源:不详 题型:解答题
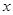 ,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表| 摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为7”出现的频数 | 1 | 9 | 14 | 24 | 26 | 37 | 58 | 82 | 109 | 150 |
| “和为7”出现的频率 | 0.10 | 0.45 | 0.47 | 0.40 | 0.29 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
 )
)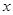 的值;
的值; 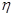 元,求
元,求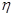 的数学期望和方差。
的数学期望和方差。查看答案和解析>>
科目: 来源:不详 题型:解答题
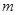 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为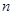 ,求
,求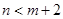 的概率.
的概率.查看答案和解析>>
科目: 来源:不详 题型:解答题


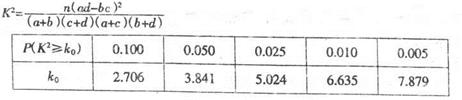
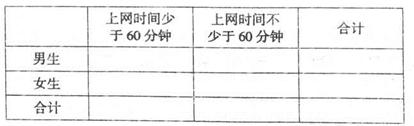 •
•
查看答案和解析>>
科目: 来源:不详 题型:解答题
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 3 | 5 | 7 | 7 | 5 | 3 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
 表示售出A、B商品的日利润值(单位:元).将频率视为概率.
表示售出A、B商品的日利润值(单位:元).将频率视为概率.查看答案和解析>>
科目: 来源:不详 题型:单选题
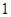 ,
,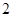 ,
,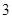 ,
,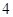 ,
,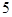 的五张卡片中任取两张,假设每张卡片被取到的概率相等,且每张卡片上只有一个数字,则取到的两张卡片上的数字之和为偶数的概率为( )
的五张卡片中任取两张,假设每张卡片被取到的概率相等,且每张卡片上只有一个数字,则取到的两张卡片上的数字之和为偶数的概率为( )A.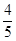 | B.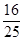 |
C.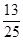 | D.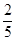 |
查看答案和解析>>
科目: 来源:不详 题型:单选题
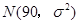 ,其中
,其中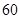 分以下的考生人数占
分以下的考生人数占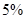 ,则数学成绩在
,则数学成绩在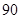 至
至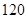 分之间的考生人数所占百分比约为 ( )
分之间的考生人数所占百分比约为 ( )A.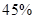 | B.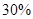 | C.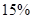 | D.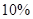 |
查看答案和解析>>
科目: 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com