
科目: 来源:不详 题型:解答题
 个红球,
个红球, 个白球(
个白球( ,且
,且 );乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜.
);乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜. 的分布列.
的分布列.查看答案和解析>>
科目: 来源:不详 题型:单选题
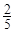 小时,种植一棵枫树苗用时
小时,种植一棵枫树苗用时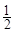 小时.完成这次植树任务需要最短时间为( )
小时.完成这次植树任务需要最短时间为( )A.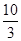 | B.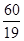 | C.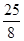 | D.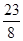 |
查看答案和解析>>
科目: 来源:不详 题型:解答题
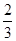 与
与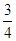 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.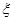 的数学期望;
的数学期望;查看答案和解析>>
科目: 来源:不详 题型:单选题

A.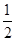 | B.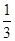 |
C. | D.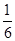 |
查看答案和解析>>
科目: 来源:不详 题型:解答题

 表示抽到“极幸福”的人数, 求
表示抽到“极幸福”的人数, 求 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目: 来源:不详 题型:解答题
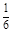 .甲、乙、丙三位同学每人购买了一瓶该饮料.
.甲、乙、丙三位同学每人购买了一瓶该饮料.查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
科目: 来源:不详 题型:解答题
| 登记所需时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
查看答案和解析>>
科目: 来源:不详 题型:单选题
| A.0.72 | B.0.89 | C.0.8 | D.0.76 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com