
科目: 来源:不详 题型:解答题
 ,4的三个形状大小完全相同的球,现从此盒中有放回地先后摸取两个球,标号分别记为x、y,求事件“
,4的三个形状大小完全相同的球,现从此盒中有放回地先后摸取两个球,标号分别记为x、y,求事件“ =
= ”的概率;
”的概率; 的概率
的概率查看答案和解析>>
科目: 来源:不详 题型:解答题
 “试剂盒”的第一时间,特别选择了知道诊断结论的5位发热病人(其中“甲流感”患者只占少数),对病情做
“试剂盒”的第一时间,特别选择了知道诊断结论的5位发热病人(其中“甲流感”患者只占少数),对病情做 了一次验证性检测.已知如果任意抽检2人,恰有1位是“甲流感”患者的概率为
了一次验证性检测.已知如果任意抽检2人,恰有1位是“甲流感”患者的概率为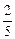 。
。 的人数
的人数 ;
;查看答案和解析>>
科目: 来源:不详 题型:解答题
 ,试验不成功的概率都是
,试验不成功的概率都是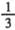 甲随机地从两套方案中选取一套进行这项试验,共试验了 3次,每次实验相互独立,且要从两套方案中等可能地选择一套.
甲随机地从两套方案中选取一套进行这项试验,共试验了 3次,每次实验相互独立,且要从两套方案中等可能地选择一套.查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
科目: 来源:不详 题型:解答题
 .现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.
.现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.查看答案和解析>>
科目: 来源:不详 题型:解答题
 ,求
,求 的分布列及
的分布列及 。
。查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com