
科目: 来源:不详 题型:解答题
 .
. )若从甲盒中任取两个球,放入乙盒中均匀后,再从乙盒中任意取出2个球放回到甲盒中,求甲盒中白球没有增加的概率;
)若从甲盒中任取两个球,放入乙盒中均匀后,再从乙盒中任意取出2个球放回到甲盒中,求甲盒中白球没有增加的概率;查看答案和解析>>
科目: 来源:不详 题型:解答题
  | 200元 | 300元 | 400元 | 500元 |
| 老年 | 0.4 | 0.3 | 0.2 | 0.1 |
| 中年 | 0.3 | 0.4 | 0.2 | 0.1 |
| 青年 | 0.3 | 0.3 | 0.2 | 0.2 |
 ,求
,求 的分布列及数学期望。
的分布列及数学期望。查看答案和解析>>
科目: 来源:不详 题型:解答题
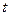 名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是
名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是 按上述分组方式得到的频率分布表。
按上述分组方式得到的频率分布表。| 分 组 | 频数 | 频率 |
| [13,14) | 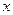 | 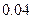 |
| [14,15) | 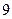 | 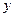 |
| [15,16) | 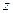 |  |
| [16,17) | 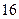 | 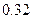 |
| [17,18] | 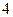 | 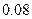 |
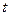 及上表中的
及上表中的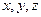 的值;
的值; 百米测试成绩,求事件“
百米测试成绩,求事件“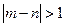 ”的
”的 概率.
概率.查看答案和解析>>
科目: 来源:不详 题型:填空题
查看答案和解析>>
科目: 来源:不详 题型:解答题
 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为 .若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
.若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响 ,求汽
,求汽 车走公路②堵车的概率P。
车走公路②堵车的概率P。 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目: 来源:不详 题型:解答题


 ,请完成上面的
,请完成上面的 列联表;
列联表; |  |  |  |
 |  |  |  |
查看答案和解析>>
科目: 来源:不详 题型:解答题
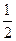 ,安排最后两道题,每题得出正确答案的概率为
,安排最后两道题,每题得出正确答案的概率为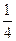 ,且每题答对与否相互独立,同时规定:每题选对得5分,不选或选错得0分.
,且每题答对与否相互独立,同时规定:每题选对得5分,不选或选错得0分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com