
科目: 来源:不详 题型:单选题
| 1 |
| x |
| g(x1)-g(x2) |
| x1-x2 |
A.g(x)=1-
| B.g(x)=x2+lnx-2 | ||||
C.g(x)=-2x-
| D.g(x)=ex(2x+
|
查看答案和解析>>
科目: 来源:不详 题型:解答题
| 2x |
| x+2 |
| 1 |
| 2 |
查看答案和解析>>
科目: 来源:广东省期中题 题型:解答题
 .
. )最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
查看答案和解析>>
科目: 来源:浙江省模拟题 题型:解答题
已知函数f(x)=ax2+lnx(a∈R)。
(1)当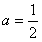 时,求f(x)在区间[1,e]上的最大值和最小值;
时,求f(x)在区间[1,e]上的最大值和最小值;
(2)如果函数g(x),f1(x),f2(x)在公共定义域D上,满足f1(x)<g(x)<f2(x),那么就称g(x)为f1(x),f2(x)的 “活动函数”。已知函数f1(x)=(a-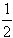 )x2+2ax+(1-a2)lnx,f2(x)=
)x2+2ax+(1-a2)lnx,f2(x)=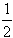 x2+2ax。
x2+2ax。
①若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“活动函数”,求a的取值范围;
②当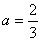 时,求证:在区间(1,+∞)上,函数f1(x),f2(x)的“活动函数”有无穷多个。
时,求证:在区间(1,+∞)上,函数f1(x),f2(x)的“活动函数”有无穷多个。
查看答案和解析>>
科目: 来源:高考真题 题型:解答题
查看答案和解析>>
科目: 来源:攀枝花二模 题型:解答题
查看答案和解析>>
科目: 来源:0110 月考题 题型:解答题
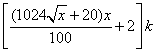 元。假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为y元。
元。假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为y元。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com