
科目: 来源:期末题 题型:解答题

查看答案和解析>>
科目: 来源:月考题 题型:解答题
查看答案和解析>>
科目: 来源:月考题 题型:解答题
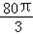 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.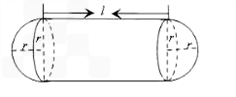
查看答案和解析>>
科目: 来源:月考题 题型:解答题
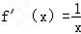 ,g(x)=f(x)+f'(x).
,g(x)=f(x)+f'(x).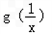 的大小关系;
的大小关系;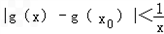 对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由.
对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由.查看答案和解析>>
科目: 来源:期末题 题型:解答题
查看答案和解析>>
科目: 来源:高考真题 题型:解答题
 与x轴正半轴相交于点A,设f(n)为该抛物线在点A处的切线在y轴上的截距。
与x轴正半轴相交于点A,设f(n)为该抛物线在点A处的切线在y轴上的截距。 成立的a的最小值;
成立的a的最小值; 与
与 的大小,并说明理由
的大小,并说明理由查看答案和解析>>
科目: 来源:期末题 题型:解答题
已知f(x)=ax﹣1nx,x∈(0,e],g(x)=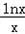 ,其中e是自然常数,a∈R.
,其中e是自然常数,a∈R.
(Ⅰ)当a=1时,研究f(x)的单调性与极值;
(Ⅱ)在(Ⅰ)的条件下,求证:f(x)>g(x)+ ;
;
(Ⅲ)是否存在实数a,使f(x)的最小值是3?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源:期末题 题型:解答题
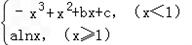 的图象过点(﹣1,2),且在点(﹣1,f(
的图象过点(﹣1,2),且在点(﹣1,f(查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com