
科目: 来源:模拟题 题型:解答题
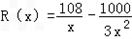 .
.查看答案和解析>>
科目: 来源:月考题 题型:解答题
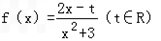 .
. ,求当x>0时,f(x)的最大值.
,求当x>0时,f(x)的最大值.查看答案和解析>>
科目: 来源:同步题 题型:解答题

查看答案和解析>>
科目: 来源:江西省模拟题 题型:解答题
查看答案和解析>>
科目: 来源:0103 模拟题 题型:解答题
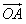 ﹑
﹑ ﹑
﹑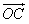 满足
满足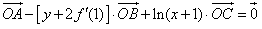 ;
;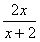 ;
;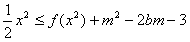 时,x∈[-1,1]及b∈[-1,1]都恒成立,求实数m的取值范围。
时,x∈[-1,1]及b∈[-1,1]都恒成立,求实数m的取值范围。 查看答案和解析>>
科目: 来源:新疆自治区月考题 题型:解答题
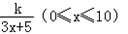 ,若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
,若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.查看答案和解析>>
科目: 来源:月考题 题型:解答题
 ,l表示扇形的弧长)
,l表示扇形的弧长)
查看答案和解析>>
科目: 来源:月考题 题型:解答题
 =
= ,并确定这样的x0的个数.
,并确定这样的x0的个数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com