练习册

  • 练习册
  • 试题
    相关习题
     0  16998  17006  17012  17016  17022  17024  17028  17034  17036  17042  17048  17052  17054  17058  17064  17066  17072  17076  17078  17082  17084  17088  17090  17092  17093  17094  17096  17097  17098  17100  17102  17106  17108  17112  17114  17118  17124  17126  17132  17136  17138  17142  17148  17154  17156  17162  17166  17168  17174  17178  17184  17192  266669 

    科目： 来源：重庆市高考真题 题型：解答题

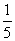    某工厂生产某种产品，已知该产品的月生产量x（吨）与每吨产品的价格p（元/吨）之间的关系式为：p=24200-x2，且生产x吨的成本为R=50000+200x（元），问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入─成本）

    查看答案和解析>>

    科目： 来源：辽宁省高考真题 题型：解答题

    甲方是一农场，乙方是一工厂，由于乙方生产须占用甲方的资源，因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入，在乙方不赔付甲方的情况下，乙方的年利润x（元）与年产量t（吨）满足函数关系，若乙方每生产一吨产品必须赔付甲方s元（以下称s为赔付价格），
    （1）将乙方的年利润w（元）表示为年产量t（吨）的函数，并求出乙方获得最大利润的年产量；
    （2）甲方每年受乙方生产影响的经济损失金额y=0.002t2（元），在乙方按照获得最大利润的产量进行生产的前提下，甲方要在索赔中获得最大净收入，应向乙方要求的赔付价格s是多少？

    查看答案和解析>>

    科目： 来源：江苏高考真题 题型：单选题

    函数f（x）=x3-3x+1在闭区间[-3，0]上的最大值、最小值分别是

    [     ]

    A.1，-1
    B.1，-17
    C.3，-17
    D.9，-19

    查看答案和解析>>

    科目： 来源：高考真题 题型：解答题

    已知函数f(x)=ln(1+x)-x，g(x)=xlnx，
    (1)求函数f(x)的最大值；
    (2)设0＜a＜b，证明：0＜g(a)+g(b)-2g()＜(b-a)ln2。

    查看答案和解析>>

    科目： 来源：专项题 题型：解答题

    某商店经销一种世博纪念品，每件产品的成本为30元，并且每卖出一件产品需向税务部门上缴5元的税收，设每件产品的日售价为x元(35≤x≤41)，根据市场调查，日销售量与ex(e为自然对数底数)成反比例，已知每件产品的日售价为40元时，日销售量为10件，
    (Ⅰ)求该商店的日利润L(x)元与每件产品的日售价x元的函数关系式；
    (Ⅱ)当每件产品的日售价为多少元时，该商品的日利润L(x)最大，并求出L(x)的最大值。

    查看答案和解析>>

    科目： 来源：黑龙江省模拟题 题型：解答题

    已知f（x）=ax3-2ax2+b（a≠0）。
    （1）求出f（x）的极值；
    （2）若f（x）在区间[-2，1]上最大值是5，最小值是-11，求f（x）的解析式。

    查看答案和解析>>

    科目： 来源：浙江省模拟题 题型：解答题

    已知函数f（x）=ax2-3x+4+2lnx（a>0）。
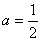    （1）当时，求函数f（x）在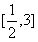上的最大值；
    （2）若f（x）在定义域上是增函数，求实数a的取值范围。

    查看答案和解析>>

    科目： 来源：陕西省模拟题 题型：解答题

    已知f（x）是定义在[-e，0）∪（0，e]上的奇函数，当x∈（0，e]时，f（x）=ax+lnx。
    （1）求f（x）的解析式；
    （2）是否存在负实数a，使得当x∈[-e，0）时，函数f（x）的最小值为3？

    查看答案和解析>>

    科目： 来源：浙江省模拟题 题型：解答题

    已知函数f（x）=x3-ax，
    （Ⅰ）当a=3时，求f（x）在[-2，2]上的最大值和最小值；
    （Ⅱ）已知函数g（x）=ax（|x+a|-1），记h（x）=f（x）-g（x）（x∈[0，2]），当函数h（x）的最大值为0时，求实数a的取值范围。

    查看答案和解析>>

    科目： 来源：湖南省高考真题 题型：解答题

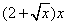    某地建一座桥，两端的桥墩已建好，这两墩相距m米，余下工程只需要建两端桥墩之间的桥面和桥墩，经预测，一个桥墩的工程费用为256万元，距离为x米的相邻两墩之间的桥面工程费用为万元。假设桥墩等距离分布，所有桥墩都视为点，且不考虑其他因素，记余下工程的费用为y万元，
    （Ⅰ）试写出y关于x的函数关系式；
    （Ⅱ）当m=640米时，需新建多少个桥墩才能使y最小？

    查看答案和解析>>

    同步练习册答案