已知函数f(x)=-x3+ax2-4的导函数. (1)当a=2时.对于任意的m∈[-1.1].求f(m)的范围, (2)若存在x0∈.使f(x0)＞0.求a的取值范围.——青夏教育精英家教网—

相关习题

0 16999 17007 17013 17017 17023 17025 17029 17035 17037 17043 17049 17053 17055 17059 17065 17067 17073 17077 17079 17083 17085 17089 17091 17093 17094 17095 17097 17098 17099 17101 17103 17107 17109 17113 17115 17119 17125 17127 17133 17137 17139 17143 17149 17155 17157 17163 17167 17169 17175 17179 17185 17193 266669

科目： 来源：0113 期末题 题型：解答题

已知函数f（x）=-x³+ax²-4（a∈R），f（x）是f′（x）的导函数。
（1）当a=2时，对于任意的m∈[-1，1]，求f（m）的范围；
（2）若存在x₀∈（0，+∞），使f（x₀）＞0，求a的取值范围。

查看答案和解析>>

科目： 来源：期末题 题型：单选题

在x∈

上，函数f（x）=x²+px+q与

在同一点取得相同的最小值，那么f（x）在

上的最大值是

[ ]

B.4
C.8
D.

查看答案和解析>>

科目： 来源：江苏高考真题 题型：解答题

请您设计一个帐篷，它下部的形状是高为1m的正六棱柱，上部的形状是侧棱长为3m的正六棱锥（如图所示）。试问当帐篷的顶点O到底面中心O₁的距离为多少时，帐篷的体积最大？

查看答案和解析>>

科目： 来源：高考真题 题型：解答题

设函数f(x)=(x+1)ln(x+1)，若对所有的x≥0，都有f(x)≥ax成立，求实数a的取值范围。

查看答案和解析>>

科目： 来源：江苏高考真题 题型：填空题

已知函数f（x）=x³-12x+8在区间[-3，3]上的最大值与最小值分别为M，m，则M-m=（）。

查看答案和解析>>

科目： 来源：北京高考真题 题型：解答题

如图，有一块半椭圆形钢板，其半轴长为2r，短半轴长为r，计划将此钢板切割成等腰梯形的形状，下底AB是半椭圆的短轴，上底CD的端点在椭圆上，记CD=2x，梯形面积为S。

（1）求面积S以x为自变量的函数式，并写出其定义域；
（2）求面积S的最大值。

查看答案和解析>>

科目： 来源：专项题 题型：填空题

若存在实常数k和b，使得函数f(x)和g(x)对其定义域上的任意实数x分别满足：f(x)≥kx+b和g(x)≤kx+b，则称直线l：y=kx+b为f(x)和g(x)的“隔离直线”。已知h(x)=x²，φ(x)=2elnx(其中e为自然对数的底数)，根据你的数学知识，推断h(x)与φ(x)间的隔离直线方程为（）。

查看答案和解析>>

科目： 来源：福建省高考真题 题型：解答题

某分公司销售某种商品，每件商品的成本为3元，并且每件商品需向总店交a元（3≤a≤5）的管理费，预计当每件商品的售价为x元（9≤x≤11）时，一年的销售量为（12-x）²万件。
（1）求分公司一年的利润L（万元）与每件商品的售价x的函数关系式L（x）；
（2）当每件商品的售价为多少元时，该分公司一年的利润L最大，并求出L的最大值M（a）。

查看答案和解析>>

科目： 来源：山东省高考真题 题型：解答题

两县城A和B相距20km，现计划在两县城外以AB为直径的半圆弧

上选择一点C建造垃圾处理厂，其对城市的影响度与所选地点到城市的的距离有关，对城A和城B的总影响度为城A与城B的影响度之和，记C点到城A的距离为x km，建在C处的垃圾处理厂对城A和城B的总影响度为y，统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比，比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比，比例系数为k，当垃圾处理厂建在

的中点时，对城A和城B的总影响度为0.065，
（1）将y表示成x的函数；
（2）讨论（1）中函数的单调性，并判断弧

上是否存在一点，使建在此处的垃圾处理厂对城A和城B的总影响度最小？若存在，求出该点到城A的距离；若不存在，说明理由。

查看答案和解析>>

科目： 来源：福建省高考真题 题型：填空题

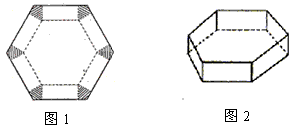
图1，将边长为1的正六边形铁皮的六个角各切去一个全等的四边形，再沿虚线折起，做成一个无盖的正六棱柱容器（图2），当这个正六棱柱容器的底面边长为（）时，其容积最大。

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学