科目： 来源：不详 题型：填空题

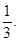．出租车司机从饭店到火车站途中有六个交通岗，假设他在各交通岗遇到红灯是相互独立的，并且概率都是 则这位司机在途中遇到红灯数ξ的方差为        . （用分数表示）

科目： 来源：不详 题型：解答题

．（本小题10分）
在一次购物抽奖活动中，假设某10张券中有一等奖券1张，可获价值50元的奖品；有二等奖券3张，每张可获价值10元的奖品；其余6张没有奖，某顾客从此10张券中任抽2张，求：（1）该顾客中奖的概率；（2）该顾客获得的奖品总价值（元）的概率分布列和期望.

科目： 来源：不详 题型：单选题

（本小题满分12分）
NBA总决赛采用“7场4胜制”，由于NBA有特殊的政策和规则，能进入决赛的球队实力都较强，因此可以认为，两个队在每一场比赛中取胜的概率相等。根据不完全统计，主办一场决赛，每一方组织者有望通过出售电视转播权、门票及零售商品、停车费、广告费等收入获取收益2000万美元（1）求比赛场数的分布列；(2)求双方组织者通过比赛获得总收益的数学期望。

科目： 来源：不详 题型：单选题

（本小题满分13分）
现有甲、乙两个项目，对甲项目投资十万元，一年后利润是1.2万元、1.18万元、1.17万元的概率分别为、、;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为,对乙项目投资十万元, 取0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量、分别表示对甲、乙两项目各投资十万元一年后的利润.
(I) 求、的概率分布和数学期望、;
(II)当时,求的取值范围.

科目： 来源：不详 题型：解答题

科目： 来源：不详 题型：解答题

科目： 来源：不详 题型：解答题

在奥运会射箭决赛中，参赛号码为1～4号的四名射箭运动员参加射箭比赛.
（Ⅰ）通过抽签将他们安排到1～4号靶位，试求恰有两名运动员所抽靶位号与其参赛号码相同的概率；
（Ⅱ）记1号、2号射箭运动员射箭的环数为（所有取值为0，1，2，3．．．，10）的概率分别为、.根据教练员提供的资料，其概率分布如下表:

	0	1	2	3	4	5	6	7	8	9	10
	0	0	0	0	0.06	0.04	0.06	0.3	0.2	0.3	0.04
	0	0	0	0	0.04	0.05	0.05	0.2	0.32	0.32	0.02

①1，2号运动员各射箭一次，求两人中至少有一人命中9环的概率；
②判断1号，2号射箭运动员谁射箭的水平高？并说明理由．

科目： 来源：不详 题型：填空题

有一批产品，其中有12件正品和4件次品，从中任取3件，若表示取到次品的个数，则E=        .

科目： 来源：不详 题型：解答题

（本小题满分12分）
甲乙两名射手互不影响地进行射击训练，根据以往的数据统计，他们设计成绩的分布列如下：

射手甲				射手乙
环数	8	9	10	环数	8	9	10
概率				概率

（Ⅰ）若甲乙两射手各射击两次，求四次射击中恰有三次命中10环的概率；
（Ⅱ）若两个射手各射击1次，记所得的环数之和为，求的分布列和期望．

科目： 来源：不详 题型：解答题

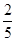（本大题9分）袋中有2个红球，n个白球，各球除颜色外均相同.已知从袋中摸出2个球均为白球的概率为，（Ⅰ）求n；（Ⅱ）从袋中不放回的依次摸出三个球，记ξ为相邻两次摸出的球不同色的次数（例如：若取出的球依次为红球、白球、白球，则ξ=1），求随机变量ξ的分布列及其数学期望Eξ.