
科目: 来源:不详 题型:解答题
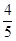 ,第二、第三种产品受欢迎的概率分别为
,第二、第三种产品受欢迎的概率分别为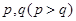 ,且不同种产品是否受欢迎相互独立.记
,且不同种产品是否受欢迎相互独立.记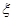 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为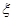 | 0 | 1 | 2 | 3 |
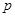 | 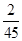 | 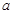 | 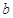 | 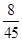 |
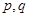 的值
的值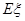 .
.查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
科目: 来源:不详 题型:解答题
 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。 ,求
,求 的分布列与数学期望。
的分布列与数学期望。查看答案和解析>>
科目: 来源:不详 题型:解答题
| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 4 | 4 | 3 | 1 |
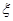 ,求随机变量
,求随机变量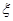 的分布列和数学期望
的分布列和数学期望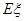 .(8分)
.(8分)查看答案和解析>>
科目: 来源:不详 题型:解答题
 层下电梯的概率
层下电梯的概率 ;
; 的数学期望.
的数学期望.查看答案和解析>>
科目: 来源:不详 题型:解答题
 视觉 视觉 | 视觉记忆能力 | ||||
| 偏低 | 中等 | 偏高 | 超常 | ||
| 听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
| 中等 | 1 | 8 | 3 |  | |
| 偏高 | 2 |  | 0 | 1 | |
| 超常 | 0 | 2 | 1 | 1 | |
 .
. 、
、 的值;
的值; ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
科目: 来源:不详 题型:解答题
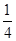 ,8∶20发出的概率为
,8∶20发出的概率为 ,8∶40发出的概率为
,8∶40发出的概率为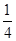 ;第二班客车在9∶00,9∶20,9∶40这三个时刻随机发出,且在9∶00发出的概率为
;第二班客车在9∶00,9∶20,9∶40这三个时刻随机发出,且在9∶00发出的概率为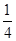 ,9∶20发出的概率为
,9∶20发出的概率为 ,9∶40发出的概率为
,9∶40发出的概率为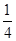 .两班客车发出时刻是相互独立的,一位旅客预计8∶10到站.求:
.两班客车发出时刻是相互独立的,一位旅客预计8∶10到站.求: 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目: 来源:不详 题型:解答题
甲部门不同岗位月工资 (元) (元) | 2200 | 2400 | 2600 | 2800 |
获得相应岗位的概率 | 0.4 | 0.3 | 0.2 | 0.1 |
乙部门不同岗位月工资 (元) (元) | 2000 | 2400 | 2800 | 3200 |
获得相应岗位的概率 | 0.4 | 0.3 | 0.2 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com