
科目: 来源:不详 题型:解答题
查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
科目: 来源:不详 题型:解答题
 ,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资. ,求
,求 的分布列及数学期望E
的分布列及数学期望E .
.查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
科目: 来源:不详 题型:解答题
 分 . 现从盒内任取3个球.
分 . 现从盒内任取3个球. 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
科目: 来源:不详 题型:解答题
 元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为
元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为 。
。 ;
;查看答案和解析>>
科目: 来源:不详 题型:解答题
 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 。
。 ,求随机变量
,求随机变量 的数学期望
的数学期望 。
。 。并指出袋中哪种颜色的球个数最少。
。并指出袋中哪种颜色的球个数最少。查看答案和解析>>
科目: 来源:不详 题型:解答题

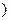 ,[50,60
,[50,60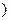 ,…[90,100]后得到如下频率分布直方图.
,…[90,100]后得到如下频率分布直方图.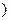 的概率;
的概率;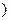 ,记为0分,在[60,100],记为1分.用X表示抽取结束后的总记分,求X的分布列和数学期望.
,记为0分,在[60,100],记为1分.用X表示抽取结束后的总记分,求X的分布列和数学期望.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com