
科目: 来源:不详 题型:解答题
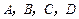 四个交通岗,其中在
四个交通岗,其中在 岗遇到红灯的概率均为
岗遇到红灯的概率均为 ,在
,在 岗遇到红灯的概率均为
岗遇到红灯的概率均为 .假设他在4个交通岗遇到红灯的事件是相互独立的,X表示他遇到红灯的次数.
.假设他在4个交通岗遇到红灯的事件是相互独立的,X表示他遇到红灯的次数. ,就会迟到,求张华不迟到的概率;(2)求EX.
,就会迟到,求张华不迟到的概率;(2)求EX.查看答案和解析>>
科目: 来源:不详 题型:解答题
| 电话同时 打入个数 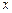 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
概率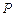 | 0.13 | 0.35 | 0.27 | 0.14 | 0.08 | 0.02 | 0.01 | 0 | 0 |
查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
科目: 来源:不详 题型:解答题
 0~6:00定为职工活动时间,并成立了行政和教师两支篮球队,但由于工作性质所限,每月(假设为4周)每支球队只能组织两次活动,且两支球队的活动时间是相互独立的。
0~6:00定为职工活动时间,并成立了行政和教师两支篮球队,但由于工作性质所限,每月(假设为4周)每支球队只能组织两次活动,且两支球队的活动时间是相互独立的。 支球队每月两次都在同一时间活动的频率;
支球队每月两次都在同一时间活动的频率; ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目: 来源:不详 题型:解答题
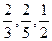 .
.查看答案和解析>>
科目: 来源:不详 题型:解答题
 分别写在六张卡片上,放在一盒子中。 (1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数卡片则停止抽取,否则继续进行,求抽取次数
分别写在六张卡片上,放在一盒子中。 (1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数卡片则停止抽取,否则继续进行,求抽取次数 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目: 来源:不详 题型:解答题


 的概率分布列及期望;若从甲、乙运动员中只能挑选一名参加某大型比赛,你认为让谁参加比较合适?
的概率分布列及期望;若从甲、乙运动员中只能挑选一名参加某大型比赛,你认为让谁参加比较合适?查看答案和解析>>
科目: 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com