已知函数f(x)＝sin xcos x＋cos 2x－，△ABC三个内角A，B，C的对边分别为a，b，c，且f(B)＝1.

(1)求角B的大小；

(2)若a＝，b＝1，求c的值．

一个袋子装有大小形状完全相同的9个球，其中5个红球编号分别为1,2,3,4,5,4个白球编号分别为1,2,3,4，从袋中任意取出3个球．

(1)求取出的3个球编号都不相同的概率；

(2)记X为取出的3个球中编号的最小值，求X的分布列与数学期望．

已知数列{an}满足a1＝3，an＋1＝an＋p·3n(n∈N*，p为常数)，a1，a2＋6，a3成等差数列．

(1)求p的值及数列{an}的通项公式；

(2)设数列{bn}满足bn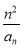＝，证明：bn≤.

如图，在矩形ABCD中，AB＝2AD＝2，O为CD的中点，沿AO将△AOD折起，使DB＝.

(1)求证：平面AOD⊥平面ABCO；

(2)求直线BC与平面ABD所成角的正弦值．

已知抛物线C：y2＝2px(p>0)，M点的坐标为(12,8)，N点在抛物线C上，且满足＝，O为坐标原点．

(1)求抛物线C的方程；

(2)以M点为起点的任意两条射线l1，l2的斜率乘积为1，并且l1与抛物线C交于A，B两点，l2与抛物线C交于D，E两点，线段AB，DE的中点分别为G，H两点．求证：直线GH过定点，并求出定点坐标．

已知函数f(x)＝(ax2＋bx＋c)ex且f(0)＝1，f(1)＝0.

(1)若f(x)在区间[0,1]上单调递减，求实数a的取值范围；

(2)当a＝0时，是否存在实数m使不等式2f(x)＋4xex≥mx＋1≥－x2＋4x＋1对任意x∈R恒成立？若存在，求出m的值，若不存在，请说明理由．

已知函数f(x)＝sin ＋2cos2x－1(x∈R)．

(1)求函数f(x)的最小正周期及单调递增区间；

(2)在△ABC中，三内角A，B，C的对边分别为a，b，c，已知函数f(x)的图象经过点，b，a，c成等差数列，且·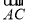＝9，求a的值．

设数列{an}的前n项和为Sn，a1＝1，且对任意正整数n，点(an＋1，Sn)在直线3x＋2y－3＝0上．

(1)求数列{an}的通项公式；

(2)是否存在实数λ，使得数列为等差数列？若存在，求出λ的值；若不存在，则说明理由．

某校为组建校篮球队，对报名同学进行定点投篮测试，规定每位同学最多投3次，每次在A或B处投篮，在A处投进一球得3分，在B处投进一球得2分，否则得0分，每次投篮结果相互独立，将得分逐次累加并用X表示，如果X的值不低于3分就认为通过测试，立即停止投篮，否则继续投篮，直到投完三次为止．投篮方案有以下两种：

方案1：先在A处投一球，以后都在B处投；

方案2：都在B处投篮．

已知甲同学在A处投篮的命中率为0.4，在B处投篮的命中率为0.6.

(1)甲同学若选择方案1，求X＝2时的概率；

(2)甲同学若选择方案2，求X的分布列和数学期望；

(3)甲同学选择哪种方案通过测试的可能性更大？请说明理由．

如图，在四棱锥P-ABCD中，已知PB⊥底面ABCD，BC⊥AB，AD∥BC，AB＝AD＝2，CD⊥PD，异面直线PA和CD所成角等于60°.

(1)求证：面PCD⊥面PBD；

(2)求直线PC和平面PAD所成角的正弦值的大小；

(3)在棱PA上是否存在一点E，使得二面角A-BE-D的余弦值为？若存在，指出点E在棱PA上的位置，若不存在，说明理由．