在△ABC中，角A，B，C的对边分别为a，b，c，已知角A＝， sin B＝3sin C.

(1)求tan C的值；

(2)若a＝，求△ABC的面积．

已知函数f(x)＝sin ωx·cos ωx＋cos 2ωx－(ω>0)，其最小正周期为.

(1)求f(x)的解析式．

(2)将函数f(x)的图象向右平移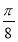个单位，再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，得到函数y＝g(x)的图象，若关于x的方程g(x)＋k＝0，在区间上有且只有一个实数解，求实数k的取值范围．

已知m＝，n＝，f(x)＝m·n，且f＝.

(1)求A的值；

(2)设α，β∈，f(3α＋π)＝，f＝－，求cos (α＋β)的值．

已知m＝(2cos x＋2sin x,1)，n＝(cos x，－y)，且m⊥n.

(1)将y表示为x的函数f(x)，并求f(x)的单调增区间；

(2)已知a，b，c分别为△ABC的三个内角A，B，C对应的边长，若f＝3，且a＝2，b＋c＝4，求△ABC的面积．

已知函数f(x)＝sincos＋sin2 (其中ω>0,0<φ<)．其图象的两个相邻对称中心的距离为，且过点.

(1)函数f(x)的解析式；

(2)在△ABC中，a，b，c分别是角A，B，C的对边，a＝，S△ABC＝2，角C为锐角．且满足f＝，求c的值．

甲、乙两人玩猜数字游戏，规则如下：

①连续竞猜3次，每次相互独立；

②每次竞猜时，先由甲写出一个数字，记为a，再由乙猜甲写的数字，记为b，已知a，b∈{0,1,2,3,4,5}，若|a－b|≤1，则本次竞猜成功；

③在3次竞猜中，至少有2次竞猜成功，则两人获奖．

求甲乙两人玩此游戏获奖的概率．

某学生参加某高校的自主招生考试，须依次参加A，B，C，D，E五项考试，如果前四项中有两项不合格或第五项不合格，则该考生就被淘汰，考试即结束；考生未被淘汰时，一定继续参加后面的考试．已知每一项测试都是相互独立的，该生参加A，B，C，D四项考试不合格的概率均为，参加第五项不合格的概率为.

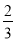(1)求该生被录取的概率；

(2)记该生参加考试的项数为X，求X的分布列和期望．

某次考试中，从甲，乙两个班各抽取10名学生的成绩进行统计分析，两班10名学生成绩的茎叶图如图所示，成绩不小于90分为及格．

(1)从每班抽取的学生中各抽取一人，求至少有一个及格的概率；

(2)从甲班10人中取两人，乙班10人中取一人，三人中及格人数记为X，求X的分布列和数学期望．

盒子中装有四张大小形状均相同的卡片，卡片上分别标有数字－1,0,1,2.称“从盒中随机抽取一张，记下卡片上的数字后并放回”为一次试验(设每次试验的结果互不影响)．

(1)在一次试验中，求卡片上的数字为正数的概率；

(2)在四次试验中，求至少有两次卡片上的数字都为正数的概率；

(3)在两次试验中，记卡片上的数字分别为X，η，试求随机变量X＝X·η的分布列与数学期望E(X)．

现有甲、乙两个靶．某射手向甲靶射击两次，每次命中的概率为，每命中一次得1分，没有命中得0分；向乙靶射击一次，命中的概率为，命中得2分，没有命中得0分，该射手每次射击的结果相互独立．假设该射手完成以上三次射击．

(1)求该射手恰好命中两次的概率；

(2)求该射手的总得分X的分布列及数学期望E(X)；

(3)求该射手向甲靶射击比向乙靶射击多击中一次的概率．