某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况，从两块地各随机抽取了10株树苗，用茎叶图表示上述两组数据，对两块地抽取树苗的高度的平均数甲，乙和中位数y甲，y乙进行比较，下面结论正确的是(　　)．

A. 甲>乙，y甲>y乙

B. 甲<乙，y甲>y乙

C. 甲<乙，y甲<y乙

D. 甲>乙，y甲<y乙

若回归直线方程的斜率的估计值是1.23，样本点的中心为(4,5)，则回归直线的方程是(　　)．

A. ＝1.23x＋4 B. ＝1.23x＋5

C. ＝1.23x＋0.08 D. 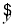＝0.08x＋1.23

某高中在校学生有2 000人．为了响应“阳光体育运动”的号召，学校开展了跑步和登山比赛活动．每人都参与而且只参与其中一项比赛，各年级参与比赛的人数情况如下表：

其中a∶b∶c＝2∶3∶5，全校参与登山的人数占总人数的.为了了解学生对本次活动的满意程度，从中抽取一个200人的样本进行调查，则从高二年级参与跑步的学生中应抽取(　)．

A．36人 B．60人 C．24人 D．30人

为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样的方法从该地区调查了500位老年人，结果如下表：

附：

K2＝

A．估计该地区老年人中，需要志愿者提供帮助的老年人的比例为10%

B．估计该地区老年人中，需要志愿者提供帮助的老年人的比例为20%

C．有99%的把握认为该地区的老年人需要志愿者提供帮助与性别有关

D．有99%的把握认为该地区的老年人需要志愿者提供帮助与性别无关

某单位200名职工的年龄分布情况如图，现要从中抽取40名职工作样本．用系统抽样的方法，将全体职工按1～200随机编号，并按编号顺序平均分为40组(1～5号，6～10号，…，196～200号)．若第5组抽出的号码为22，则第8组抽出的号码应是________．若用分层抽样的方法，则40岁以下年龄段应抽取________人．

某市为增强市民的节约粮食意识，面向全市征召义务宣传志愿者，现从符合条件的志愿者中随机抽取100名按年龄分组：第1组[20,25)，第2组[25,30)，第3组[30,35)，第4组[35,40)，第5组[40,45]，得到的频率分布直方图如图所示，若用分层抽样的方法从第3,4,5组中共抽取了12名志愿者参加10月16日的“世界粮食日”宣传活动，则从第4组中抽取的人数为________．

为了调查某地居民的年收入x(单位：万元)和年饮食支出y(单位：万元)之间的关系，用分层抽样的方法从该地调查了若干户家庭，调查显示年收入x与年饮食支出y具有线性相关关系，并由调查数据得到y对x的回归直线方程为＝0.254x＋0.321.由回归直线方程可知，家庭年收入每增加1万元，年饮食支出增加________万元．

对大于或等于2的自然数m的n次方幂有如下分解式：

22＝1＋3　32＝1＋3＋5　42＝1＋3＋5＋7…

23＝3＋5　33＝7＋9＋11…

24＝7＋9…

此规律，54的分解式中的第三个数为________．

类比正弦定理，如图，在三棱柱ABC-A1B1C1中，二面角B-AA1-C，C-BB1-A，B-CC1-A的平面角分别为α，β，γ，则有________．

有4名优秀学生A，B，C，D全部被保送到甲、乙、丙3所学校，每所学校至少去一名，且A生不去甲校，则不同的保送方案有(　　)．

A．24种 B．30种 C．36种 D．48种