(1－)20的二项展开式中，x的系数与x9的系数之差为 ________.

从某小区抽取100户居民进行月用电量调查，发现其用电量都在50至350度之间，频率分布直方图如图所示．

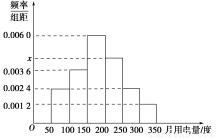
(1)直方图中x的值为 ________；

(2)在这些用户中，用电量落在区间[100,250]内的户数为________．

在区间[－2,4]上随机地取一个数x，若x满足|x|≤m的概率为，则m＝________.

由正整数组成的一组数据x1，x2，x3，x4，其平均数和中位数都是2，且标准差等于1，则这组数据为________．(从小到大排列)

某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数.

(1)根据茎叶图计算样本均值；

(2)日加工零件个数大于样本均值的工人为优秀工人．根据茎叶图推断该车间12名工人中有几名优秀工人？

(3)从该车间12名工人中，任取2人，求恰有1名优秀工人的概率．

某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品．现用两种新配方(分别称为A配方和B配方)做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：

A配方的频数分布表

B配方的频数分布表

(1)分别估计用A配方，B配方生产的产品的优质品率；

(2)已知用B配方生产的一件产品的利润y(单位：元)与其质量指标值t的关系式为y＝从用B配方生产的产品中任取一件，其利润记为X(单位：元)，求X的分布列及数学期望．(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)

为备战2016年奥运会，甲、乙两位射击选手进行了强化训练．现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次，记录如下：

甲：8.3,9.0,7.9,7.8,9.4,8.9,8.4,8.3；

乙：9.2,9.5,8.0,7.5,8.2,8.1,9.0,8.5.

(1)画出甲、乙两位选手成绩的茎叶图；

(2)现要从中选派一人参加奥运会封闭集训，从统计学角度，你认为派哪位选手参加合理？简单说明理由；

(3)若将频率视为概率，对选手乙在今后的三次比赛成绩进行预测，记这三次成绩中不低于8.5分的次数为ξ，求ξ的分布列及均值E(ξ)．

受轿车在保修期内维修费等因素的影响，企业生产每辆轿车的利润与该轿车首次出现故障的时间有关．某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年．现从该厂已售出的两种品牌轿车中各随机抽取50辆，统计数据如下：

将频率视为概率，解答下列问题：

(1)从该厂生产的甲品牌轿车中随机抽取一辆，求其首次出现故障发生在保修期内的概率．

(2)若该厂生产的轿车均能售出，记生产一辆甲品牌轿车的利润为X1，生产一辆乙品牌轿车的利润为X2，分别求X1，X2的分布列．

(3)该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌的轿车．若从经济效益的角度考虑，你认为应生产哪种品牌的轿车？说明理由．

复数在复平面上的对应点在(　　)．

A．第一象限 B．第二象限 C．第三象限 D．第四象限

若集合M＝{y|y＝2－x}，P＝{y|y＝}，则M∩P＝(　　)．

A．{y|y>1} B．{ y|y≥1} C．{ y|y >0} D．{ y|y≥0}