
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:选择题
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( ).
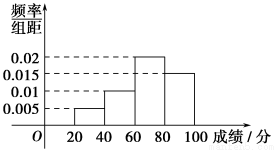
A.45 B.50 C.55 D.60
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:选择题
随机询问100名性别不同的大学生是否爱好踢毽子运动,得到如下的列联表:
| 男 | 女 | 总计 |
爱好 | 10 | 40 | 50 |
不爱好 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
附表:
P(K2≥k0) | 0.10 | 0.05 | 0.025 |
k0 | 2.706 | 3.841 | 5.024 |
经计算,统计量K2=4.762,参照附表,得到的正确结论是( ).
A.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”
C.有97.5%以上的把握认为“爱好该项运动与性别有关”
D.有97.5%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:选择题
已知P是△ABC所在平面内一点, +2
+2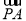 =0,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( ).
=0,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( ).
A.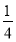 B.
B.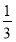 C.
C.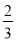 D.
D.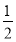
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:填空题
某校开展“爱我海西、爱我家乡”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是________.

查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:填空题
在2013年3月15日这天,郑州市物价部门对本市5家商场某商品一天的销售量及其价格进行了调查,5家商场某商品的销售价格x(元)与销售量y(件)之间的一组数据如下表:
价格x | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y | 11 | 10 | 8 | 6 | 5 |
作出散点图,可知销售量y与价格x之间具有线性相关关系,其线性回归方程是 =-3.2x+
=-3.2x+ 则实数
则实数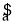 的值是________.
的值是________.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:填空题
利用计算机产生0~1之间的均匀随机数a,则事件“3a-1>0”发生的概率为________.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:解答题
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.

(1)根据茎叶图计算样本均值;
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:解答题
袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子中随机抽取1个小球,取到标号为2的小球的概率是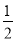 .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:解答题
为了解某班学生喜爱打篮球是否与性别有关,对本班48人进行了问卷调查得到了如下的2×2列联表:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 |
男生 |
| 6 |
|
女生 | 10 |
|
|
合计 |
|
| 48 |
已知在全班48人中随机抽取1人,抽到喜爱打篮球的学生的概率为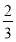 .
.
(1)请将上面的2×2列联表补充完整(不用写计算过程);
(2)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为X,求X的分布列与数学期望.
下面的临界值表供参考:
P(χ2≥x0)或 P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
x0(或k0) | 2.706 | 3.841 | 6.635 | 7.879 |
(参考公式)χ2=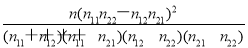 ,其中n=n11+n12+n21+n22或K2=
,其中n=n11+n12+n21+n22或K2=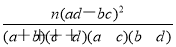 ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练18练习卷(解析版) 题型:选择题
甲射击命中目标的概率是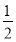 ,乙命中目标的概率是
,乙命中目标的概率是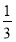 ,丙命中目标的概率是
,丙命中目标的概率是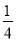 .现在三人同时射击目标,则目标被击中的概率为( ).
.现在三人同时射击目标,则目标被击中的概率为( ).
A.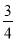 B.
B.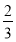 C.
C.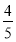 D.
D. 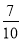
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com