
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:填空题
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是________.

查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:填空题
已知正四棱锥P-ABCD的侧棱与底面所成角为60°,M为PA中点,连接DM,则DM与平面PAC所成角的大小是________.
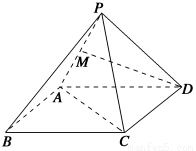
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:解答题
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
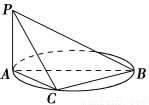
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C?PB?A的余弦值.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:解答题
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD.

(1)求证:PC⊥BD;
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD的体积取到最大值.
①求此时四棱锥E-ABCD的高;
②求二面角A-DE-B的正弦值的大小.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:解答题
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.

(1)证明B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:选择题
已知倾斜角为α的直线l与直线x-2y+2=0平行,则tan 2α的值为( ).
A.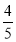 B.
B. C.
C.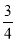 D.
D.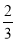
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:选择题
“a=b”是“直线y=x+2与圆(x-a)2+(x-b)2=2相切”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:选择题
已知圆(x-a)2+(y-b)2=r2的圆心为抛物线y2=4x的焦点,且与直线3x+4y+2=0相切,则该圆的方程为( ).
A.(x-1)2+y2=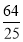 B.x2+(y-1)2=
B.x2+(y-1)2=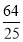
C.(x-1)2+y2=1 D.x2+(y-1)2=1
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:选择题
已知圆的方程为x2+y2-6x-8y=0,设该圆中过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积是( ).
A.10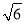 B.20
B.20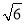 C.30
C.30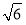 D.40
D.40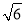
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:选择题
直线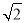 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
A.0 B. C.
C. -1 D.
-1 D. +1
+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com