
科目: 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:选择题
已知数列{an}的前n项和Sn满足:Sn+Sm=Sn+m,且a1=1,那么a11=( ).
A.1 B.9 C.10 D.55
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:选择题
已知等差数列{an}的前n项和为Sn,a5=5,S5=15,则数列 的前200项和为 ( ).
的前200项和为 ( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:选择题
已知{an}为等比数列,a4+a7=2,a2·a9=-8,则a1+a10= ( ).
A.7 B.5 C.-5 D.-7
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:选择题
已知数列{an}为等比数列,Sn是它的前n项和,若a2·a3=2a1,且a4与2a7的等差中项为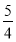 ,则S6= ( ).
,则S6= ( ).
A.35 B.33 C.31 D. 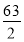
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:选择题
等比数列{an}的前n项和公式Sn,若2S4=S5+S6,则数列{an}的公比q的值为 ( ).
A.-2或1 B.-1或 2 C.-2 D.1
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:填空题
已知等比数列{an}为递增数列,且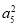 =a10,2(an+an+2)=5an+1,则a2n=________.
=a10,2(an+an+2)=5an+1,则a2n=________.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:填空题
设1=a1≤a2≤…≤a7,其中a1,a3,a5,a7成公比为q的等比数列,a2、a4、a6成公差为1的等差数列,则q的取值范围是________.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:填空题
记[x]为不超过实数x的最大整数.例如,[2]=2,[1.5]=1,[-0.3]=-1.设a为正整数,数列{xn}满足x1=a,xn+1= (n∈N*).现有下列命题:
(n∈N*).现有下列命题:
①当a=5时,数列{xn}的前3项依次为5,3,1;
②对数列{xn}都存在正整数k,当n≥k时总有xn=xk;
③当n≥1时,xn>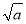 -1;
-1;
④对某个正整数k,若xk+1≥xk,则xk=[ ].
].
其中的真命题有________.(写出所有真命题的编号)
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:解答题
已知等差数列{an}的前n项和为Sn,n∈N*,且a2=3,点(10,S10)在直线y=10x上.
(1)求数列{an}的通项公式;
(2)设bn=2an+2n,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:解答题
已知Sn是数列{an}的前n项和,且an=Sn-1+2(n≥2),a1=2.
(1)求数列{an}的通项公式.
(2)设bn=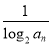 ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
对于任意的正整数n,有Tn>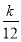 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com