已知函数f(x)＝，x∈[－1,1]，函数g(x)＝[f(x)]2－2af(x)＋3的最小值为h(a)．

(1)求h(a)；

(2)是否存在实数m、n同时满足下列条件：

①m＞n＞3；

②当h(a)的定义域为[n，m]时，值域为[n2，m2]？若存在，求出m、n的值；若不存在，说明理由．

若曲线y＝2x2的一条切线l与直线x＋4y－8＝0垂直，则切线l的方程为(　　)．　　　　　　　　　　　　　　　　　　

A．x＋4y＋3＝0 B．x＋4y－9＝0

C．4x－y＋3＝0 D．4x－y－2＝0

函数f(x)＝exsin x在区间上的值域为(　　)．

已知函数y＝f(x)，其导函数y＝f′(x)的图象如图所示，则y＝f(x) (　　)．

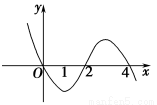
A．在(－∞，0)上为减函数

B．在x＝0处取极小值

C．在(4，＋∞)上为减函数

D．在x＝2处取极大值

设f(x)在R上可导，其导数为f′(x)，给出下列四组条件：

①p：f(x)是奇函数，q：f′(x)是偶函数；

②p：f(x)是以T为周期的函数，q：f′(x)是以T为周期的函数；

③p：f(x)在区间(－∞，＋∞)上为增函数，q：f′(x)＞0在(－∞，＋∞)恒成立；

④p：f(x)在x0处取得极值，q：f′(x0)＝0.

由以上条件中，能使p⇒q成立的序号为 (　　)．

A．①②③ B．①②④ C．①③④ D．②③④

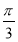由直线x＝－，x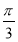＝，y＝0与曲线y＝cos x所围成的封闭图形的面积为________．

函数f(x)＝x(a＞0)的单调递减区间是________．

已知函数f(x)＝x(x－1)(x－2)(x－3)(x－4)(x－5)，则f′(0)＝________.

甲方是一农场，乙方是一工厂．由于乙方生产需占用甲方的资源，因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入，在乙方不赔付甲方的情况下，乙方的年利润x(元)与年产量t(吨)满足函数关系x＝2 000.若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格)．

(1)将乙方的年利润w(元)表示为年产量t(吨)的函数，并求出乙方获得最大利润的年产量；

(2)甲方每年受乙方生产影响的经济损失金额y＝0.002t2(元)，在乙方按照获得最大利润的产量进行生产的前提下，甲方要在索赔中获得最大净收入，应向乙方要求的赔付价格S是多少？

已知f(x)＝xln x，g(x)＝x3＋ax2－x＋2.

(1)求函数f(x)的单调区间；

(2)求f(x)在区间[t，t＋2](t＞0)上的最小值；

(3)对一切的x∈(0，＋∞)，2f(x)＜g′(x)＋2恒成立，求实数a的取值范围．