
科目: 来源:2014年高考数学(理)二轮复习1-2算法与程序框图等练习卷(解析版) 题型:解答题
若函数f(x)对任意的实数x1,x2∈D,均有|f(x2)-f(x1)|≤|x2-x1|,则称函数f(x)是区间D上的“平缓函数”.
(1)判断g(x)=sin x和h(x)=x2-x是不是实数集R上的“平缓函数”,并说明理由;
(2)若数列{xn}对所有的正整数n都有|xn+1-xn|≤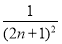 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|<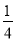 .
.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(解析版) 题型:选择题
函数y= 的定义域是( ).
的定义域是( ).
A.[- ,-1)∪(1,
,-1)∪(1, ] B.(-
] B.(- ,-1)∪(1,
,-1)∪(1, )
)
C.[-2,-1)∪(1,2] D.(-2,-1)∪(1,2)
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(解析版) 题型:选择题
已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x-3,则f(-2)=( ).
A.1 B.-1 C. 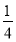 D.-
D.-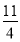
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(解析版) 题型:选择题
直线y=x与函数f(x)= 的图象恰有三个公共点,则实数m的取值范围是 ( ).
的图象恰有三个公共点,则实数m的取值范围是 ( ).
A.[-1,2) B.[-1,2] C.[2,+∞) D.(-∞,-1]
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(解析版) 题型:选择题
设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围是 ( ).
A. 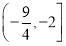 B.[-1,0] C.(-∞,-2] D.
B.[-1,0] C.(-∞,-2] D. 
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(解析版) 题型:填空题
已知函数f(x)= ,若函数g(x)=f(x)-k有两个不同的零点,则实数k的取值范围是________.
,若函数g(x)=f(x)-k有两个不同的零点,则实数k的取值范围是________.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(解析版) 题型:填空题
已知定义在R上的函数y=f(x)满足条件f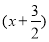 =-f(x),且函数y=f
=-f(x),且函数y=f 为奇函数,给出以下四个命题:
为奇函数,给出以下四个命题:
(1)函数f(x)是周期函数;
(2)函数f(x)的图象关于点 对称;
对称;
(3)函数f(x)为R上的偶函数;
(4)函数f(x)为R上的单调函数.
其中真命题的序号为________.(写出所有真命题的序号)
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(解析版) 题型:解答题
某养殖厂需定期购买饲料,已知该厂每天需要饲料200千克,每千克饲料的价格为1.8元,饲料的保管费与其他费用平均每千克每天0.03元,购买饲料每次支付运费300元.
(1)求该厂多少天购买一次饲料才能使平均每天支付的总费用最少;
(2)若提供饲料的公司规定,当一次购买饲料不少于5吨时,其价格可享受八五折优惠(即原价的85%).问:该厂是否应考虑利用此优惠条件?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com