
科目: 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:填空题
如图,PA⊥⊙O所在的平面,AB是⊙O的直径,C是⊙O上的一点,E,F分别是点A在PB,PC上的射影,给出下列结论:

①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC.其中正确命题的序号是________.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:填空题
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是________(写出所有正确命题的编号).

①当0<CQ< 时,S为四边形;
时,S为四边形;
②当CQ= 时,S为等腰梯形;
时,S为等腰梯形;
③当 <CQ<1时,S为六边形;
<CQ<1时,S为六边形;
④当CQ=1时,S的面积为 .
.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:解答题
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.

(1)求证:BC⊥平面PAC;
(2)设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:解答题
在直角梯形ABCD中,AB∥CD,AD⊥AB,CD=2AB=4,AD= ,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.
,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.

(1)求证:CO⊥平面ABED;
(2)问∠CEO(记为θ)多大时,三棱锥C-AOE的体积最大,最大值为多少.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:解答题
如图,在三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
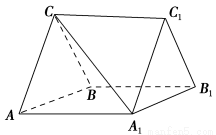
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C=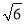 ,求三棱柱ABC-A1B1C1的体积;
,求三棱柱ABC-A1B1C1的体积;
(3)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C与平面BB1C1C所成角的正弦值.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(解析版) 题型:选择题
在正方体ABCD-A1B1C1D1中,M,N分别为棱AA1和BB1的中点,则sin〈 ,
, 〉的值为 ( ).
〉的值为 ( ).
A.  B.
B. C.
C.  D.
D.
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(解析版) 题型:选择题
如图所示,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( ).

A.  B.
B. C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(解析版) 题型:选择题
如图,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN= ,则MN与平面BB1C1C的位置关系是( ).
,则MN与平面BB1C1C的位置关系是( ).

A.相交 B.平行 C.垂直 D.不能确定
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(解析版) 题型:选择题
过正方形ABCD的顶点A,引PA⊥平面ABCD.若PA=BA,则平面ABP和平面CDP所成的二面角的大小是( ).

A.30° B.45° C.60° D.90°
查看答案和解析>>
科目: 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(解析版) 题型:选择题
正三棱柱ABC-A1B1C1的棱长都为2,E,F,G为AB,AA1,A1C1的中点,则B1F与平面GEF所成角的正弦值为( ).
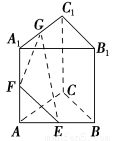
A.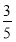 B.
B.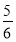 C.
C.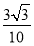 D.
D.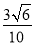
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com