已知函数f(x)＝x3＋ax2－bx(a，b∈R)，若y＝f(x)在区间[－1,2]上是单调减函数，则a＋b的最小值为______．

函数f(x)的定义域为D，若满足①f(x)在D内是单调函数，②存在[a，b]⊆D，使f(x)在[a，b]上的值域为[－b，－a]，那么y＝f(x)叫做对称函数，现有f(x)＝－k是对称函数，那么k的取值范围是________．

利民工厂某产品的年产量在100吨至300吨之间，年生产的总成本y(万元)与年产量x(吨)之间的关系可近似地表示为y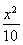＝－30x＋4 000，则每吨的成本最低时的年产量为________．

已知函数f(x)的定义域为[－1,5]，部分对应值如下表，f(x)的导函数y＝f′(x)的图象如图，下列关于函数f(x)的四个命题：

①函数y＝f(x)是周期函数；

②函数f(x)在[0,2]上是减函数；

③如果当x∈[－1，t]时，f(x)的最大值是2，那么t的最大值为4；

④当1<a<2时，函数y＝f(x)－a有4个零点．其中真命题的个数是________．

若a>1，设函数f(x)＝ax＋x－4的零点为m，函数g(x)＝logax＋x－4的零点为n，则＋的最小值为________．

对函数f(x)＝xsin x，现有下列命题：①函数f(x)是偶函数；②函数f(x)的最小正周期是2π；③点(π，0)是函数f(x)的图象的一个对称中心；④函数f(x)在区间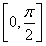上单调递增，在区间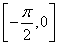上单调递减．其中是真命题的是________．(写出所有真命题的序号)

已知函数f(x)＝.

(1)确定y＝f(x)在(0，＋∞)上的单调性；

(2)若a>0，函数h(x)＝xf(x)－x－ax2在(0,2)上有极值，求实数a的取值范围．

某厂生产某种产品的年固定成本为250万元，每生产x千件，需另投入成本为C(x)．当年产量不足80千件时，C(x)＝x2＋10x(万元)；当年产量不小于80千件时，C(x)＝51x＋－1 450(万元)，每件商品售价为0.05万元，通过市场分析，该厂生产的商品能全部售完．

(1)写出年利润L(万元)关于年产量x(千件)的函数解析式；

(2)当年产量为多少千件时，该厂在这一商品的生产中所获利润最大？

已知函数f(x)＝aln(2x＋1)＋bx＋1.

(1)若函数y＝f(x)在x＝1处取得极值，且曲线y＝f(x)在点(0，f(0))处的切线与直线2x＋y－3＝0平行，求a的值；

(2)若b＝，试讨论函数y＝f(x)的单调性．

已知二次函数f(x)的二次项系数为a，且不等式f(x)＞2x的解集为(－1,3)．

(1)若函数g(x)＝xf(x)在区间内单调递减，求a的取值范围；

(2)当a＝－1时，证明方程f(x)＝2x3－1仅有一个实数根；

(3)当x∈[0,1]时，试讨论|f(x)＋(2a－1)x＋3a＋1|≤3成立的充要条件．