将图(1)中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四面体ABCD(如图(2))，则在空间四面体ABCD中，AD与BC的位置关系是(　　)

A．相交且垂直 B．相交但不垂直

C．异面且垂直 D．异面但不垂直

已知E，F，G，H是空间四点，命题甲：E，F，G，H四点不共面，命题乙：直线EF和GH不相交，则甲是乙成立的________条件．

如图，AB为圆O的直径，点C在圆周上(异于点A，B)，直线PA垂直于圆O所在的平面，点M为线段PB的中点．有以下四个命题：

①PA∥平面MOB；②MO∥平面PAC；③OC⊥平面PAC；④平面PAC⊥平面PBC.

其中正确的命题是________(填上所有正确命题的序号)．

如图，正方体ABCD－A1B1C1D1的棱长为1，点M∈AB1，N∈BC1，且AM＝BN≠，有以下四个结论：

①AA1⊥MN；②A1C1∥MN；③MN∥平面A1B1C1D1；④MN与A1C1是异面直线．其中正确命题的序号是________．(注：把你认为正确命题的序号都填上)

已知四棱锥P－ABCD中，底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD＝2EC.

(1)求证：BE∥平面PDA；

(2)若N为线段PB的中点，求证：NE⊥平面PDB.

如图，在三棱锥S－ABC中，平面SAB⊥平面SBC，AB⊥BC，AS＝AB.过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点．

求证：(1)平面EFG∥平面ABC；(2)BC⊥SA.

如图，点C是以AB为直径的圆上的一点，直角梯形BCDE所在平面与圆O所在平面垂直，且DE∥BC，DC⊥BC，DE＝BC.

(1)证明：EO∥平面ACD；

(2)证明：平面ACD⊥平面BCDE.

如图四棱柱ABCD－A1B1C1D1的底面ABCD是正方形，O是底面中心，A1O⊥底面ABCD，AB＝AA1＝.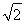

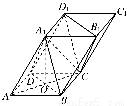
(1)证明：平面A1BD∥平面CD1B1；

(2)求三棱柱ABD－A1B1D1的体积．

如图，在三棱柱ABC－A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，AA1＝AB＝2，BC＝3.

(1)求证：AB1∥平面BC1D；

(2)求四棱锥B－AA1C1D的体积．

如图，在四棱锥P－ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD是等边三角形，已知AD＝4，BD＝4，AB＝2CD＝8.

(1)设M是PC上的一点，证明：平面MBD⊥平面PAD；

(2)当M点位于线段PC什么位置时，PA∥平面MBD?

(3)求四棱锥P－ABCD的体积．