在四棱锥P－ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC的中点，又∠CAD＝30°，PA＝AB＝4，点N在线段PB上，且＝.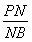

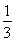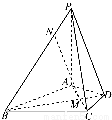
(1)求证：BD⊥PC；

(2)求证：MN∥平面PDC；

(3)设平面PAB∩平面PCD＝l，试问直线l是否与直线CD平行，请说明理由．

已知数列{an}的相邻两项an，an＋1是关于x的方程x2－2nx＋bn＝0的两根，且a1＝1.

(1)求证：数列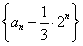是等比数列；

(2)求数列{an}的前n项和Sn；

(3)设函数f(n)＝bn－t·Sn(n∈N*)，若f(n)＞0对任意的n∈N*都成立，求t的取值范围．

某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩(满分100分，成绩均为不低于40分的整数)分成六段：[40,50)，[50,60)，…，[90,100]后得到如图所示的频率分布直方图．

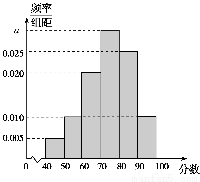
(1)求图中实数a的值；

(2)若该校高一年级共有学生640人，试估计该校高一年级期中考试数学成绩不低于60分的人数；

(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生，求这2名学生的数学成绩之差的绝对值不大于10的概率．

已知m＝(2cos x＋2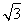sin x,1)，n＝(cos x，－y)，且m⊥n.

(1)将y表示为x的函数f(x)，并求f(x)的单调递增区间；

(2)已知a，b，c分别为△ABC的三个内角A，B，C对应的边长，若f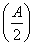＝3，且a＝2，b＋c＝4，求△ABC的面积．

如图，在几何体ABCDE中，AB＝AD＝2，AB⊥AD，AE⊥平面ABD，M为线段BD的中点，MC∥AE，且AE＝MC＝.

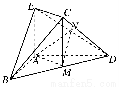
(1)求证：平面BCD⊥平面CDE；

(2)若N为线段DE的中点，求证：平面AMN∥平面BEC.

设角A，B，C为△ABC的三个内角．

(1)设f(A)＝sin A＋2sin 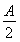，当A取A0时，f(A)取极大值f(A0)，试求A0和f(A0)的值；

(2)当A取A0时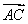，·＝－1，求BC边长的最小值．

已知四棱锥P－ABCD的正视图是一个底边长为4，腰长为3的等腰三角形，如图分别是四棱锥P－ABCD的侧视图和俯视图．

(1)求证：AD⊥PC；

(2)求四棱锥P－ABCD的侧面PAB的面积．

设L为曲线C：y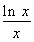＝在点(1,0)处的切线．

(1)求L的方程；

(2)证明：除切点(1,0)之外，曲线C在直线L的下方．

在平面直角坐标系xOy中，O为坐标原点，A(－2,0)，B(2,0)，点P为动点，且直线AP与直线BP的斜率之积为－.

(1)求动点P的轨迹C的方程；

(2)过点D(1,0)的直线l交轨迹C于不同的两点M，N，△MON的面积是否存在最大值？若存在，求出△MON的面积的最大值及相应的直线方程；若不存在，请说明理由．

已知函数f(x)＝(ax2－2x＋a)·e－x.

(1)当a＝1时，求函数f(x)的单调区间；

(2)设g(x)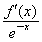＝－－a－2，h(x)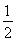＝x2－2x－ln x，若x＞1时总有g(x)＜h(x)，求实数a的取值范围．