在空间中:①若四点不共面,则这四点中任何三点都不共线;

②若两条直线没有公共点,则这两条直线是异面直线.以上两个命题中,逆命题为真命题的是　　　　　　.

已知集合A={y|y=x2-x+1,x∈[,2]},B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分条件,求实数m的取值范围.

函数f(x)=|x|和g(x)=x(2-x)的递增区间依次是(　　)

(A)(-∞,0],(-∞,1] (B)(-∞,0],[1,+∞)

(C)[0,+∞),(-∞,1] (D)[0,+∞),[1,+∞)

给定函数①y=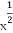,②y=lo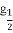(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上是单调递减的函数的序号是(　　)

(A)①② (B)②③ (C)③④ (D)①④

函数f(x)=1-(　　)

(A)在(-1,+∞)上单调递增

(B)在(1,+∞)上单调递增

(C)在(-1,+∞)上单调递减

(D)在(1,+∞)上单调递减

若函数y=ax与y=-在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是(　　)

(A)增函数 (B)减函数 (C)先增后减 (D)先减后增

已知函数f(x)=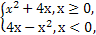若f(2-a2)>f(a),则实数a的取值范围是(　　)

(A)(-∞,-1)∪(2,+∞)

(B)(-1,2)

(C)(-2,1)

(D)(-∞,-2)∪(1,+∞)

已知函数f(x)=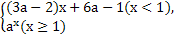单调递减,那么实数a的取值范围是(　　)

(A)(0,1) (B)(0,)

(C)[,) (D)[,1)

已知函数y=f(x)满足:对任意的x1<x2≤-1,[f(x2)-f(x1)](x2-x1)>0恒成立,则f(-2),f(-),f(-1)的大小关系为(　　)

(A)f(-2)<f(-)<f(-1)

(B)f(-2)>f(-)>f(-1)

(C)f(-2)>f(-1)>f(-)

(D)f(-)>f(-2)>f(-1)

定义在R上的函数f(x)满足f(x+y)=f(x)+f(y),当x<0时,f(x)>0,则函数f(x)在[a,b]上有(　　)

(A)最小值f(a) (B)最大值f(b)

(C)最小值f(b) (D)最大值f()